题目内容
14.将正方形ABCD折叠,使顶点A与CD边上的点M重合,折痕交AD于E,交BC于F,边AB折叠后与BC边交于点G.如果M为CD边的中点,且DE=6,求正方形ABCD的面积.分析 设DM为x,则根据折叠知道EM=EA=2x-6,然后在Rt△DEM中就可以求出x,继而求出AD的长,即可求出面积.
解答 解: 如图所示:
如图所示:
设DM=x,则AD=DC=2x,EM=EA=2x-6,
在Rt△DEM中,∠D=90°,
∴DE2+DM2=EM2
即62+x2=(2x-6)2
解得:x=8,或x=0(舍去),
∴AD=16,
∴正方形ABCD的面积=162=256.
点评 本题考查翻折变换及正方形的性质、勾股定理;熟练掌握正方形的性质,由勾股定理得出方程是解决问题的关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
5.下列各组数中,不是互为相反意义的量的是( )
| A. | 向东走20千米与向西走15千米 | B. | 收入200元与亏损30元 | ||
| C. | 超过0.05mm与不足0.03mm | D. | 上升10米和下降7米 |
2.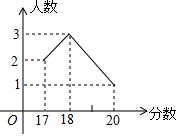 某校6名学生的某次竞赛成绩统计如图,则这组数据的众数、中位数、方差依次是( )
某校6名学生的某次竞赛成绩统计如图,则这组数据的众数、中位数、方差依次是( )
 某校6名学生的某次竞赛成绩统计如图,则这组数据的众数、中位数、方差依次是( )
某校6名学生的某次竞赛成绩统计如图,则这组数据的众数、中位数、方差依次是( )| A. | 18,17.5,5 | B. | 18,17.5,3 | C. | 18,18,3 | D. | 18,18,1 |
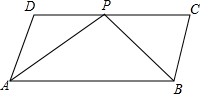 如图,ABCD是平行四边形,P是CD上一点,且AP和BP分别平分∠DAB和∠CBA.
如图,ABCD是平行四边形,P是CD上一点,且AP和BP分别平分∠DAB和∠CBA.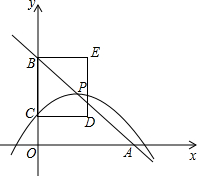 如图,在平面直角坐标系中,直线y=-x+4与x轴、y轴分别交于点A、B,抛物线y=-$\frac{1}{3}$(x-m)2+n的顶点P在直线y=-x+4上,与y轴交于点C(点P、C不与点B重合),以BC为边作矩形BCDE,且CD=2,点P、D在y轴的同侧.
如图,在平面直角坐标系中,直线y=-x+4与x轴、y轴分别交于点A、B,抛物线y=-$\frac{1}{3}$(x-m)2+n的顶点P在直线y=-x+4上,与y轴交于点C(点P、C不与点B重合),以BC为边作矩形BCDE,且CD=2,点P、D在y轴的同侧.