Question

2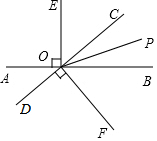．如图，直线AB与CD相交于点O，OP是∠BOC的平分线，OE⊥AB，OF⊥CD．
（1）图中除直角外，还有相等的角吗？请写出两对：
①∠COP=∠BOP；②∠AOD=∠COB．
（2）如果∠AOD=40°，
①那么根据对顶角相等，可得∠BOC=40度．
②因为OP是∠BOC的平分线，所以∠COP=$\frac{1}{2}$∠BOC=20度．
③求∠POF的度数．

Answer 1

分析 （1）根据角平分线的性质和对顶角来填空；
（2）①根据对顶角相等可得∠BOC的度数；
②根据角平分线的性质求得∠COP=$\frac{1}{2}$∠BOC=20°；
③根据垂直的定义求得∠POF的度数．

解答 解：（1）①∵OP是∠BOC的平分线，
∴∠COP=∠BOP．
②∵直线AB与CD相交于点O，
∴∠AOD=∠COB．

（2）①∵∠AOD=40°，
∴根据对顶角相等，可得∠BOC=40°；
②因为OP是∠BOC的平分线，所以∠COP=$\frac{1}{2}$∠BOC=20度．
③∵OF⊥CD，
∴∠COF=90度，
∴∠POF=70度．   
故答案是：∠COP=∠BOP、∠AOD=∠COB；对顶角相等，40；20；

点评 本题考查了垂直的定义，对顶角以及角平分线的定义．解题时一定要数形结合．