题目内容
9.化简与计算:(1)$\sqrt{12}-{(2014-\sqrt{5})^0}+|{\sqrt{3}-1}$|
(2)$(\sqrt{2}-\sqrt{6})(1+\sqrt{3})$
(3)已知m=1+$\sqrt{2}$,n=1-$\sqrt{2}$,求代数式$\sqrt{{m}^{2}+{n}^{2}-3mn}$的值.
分析 (1)根据零指数幂和二次根式的加减法可以解答本题;
(2)根据多项式乘多项式可以解答本题;
(3)根据m、n的值可以求得m-n的值与mn的值,从而可以解答本题.
解答 解:(1)$\sqrt{12}-(2014-\sqrt{5})^{0}+|\sqrt{3}-1|$
=2$\sqrt{3}-1+\sqrt{3}-1$
=$3\sqrt{3}-2$;
(2)$(\sqrt{2}-\sqrt{6})(1+\sqrt{3})$
=$\sqrt{2}+\sqrt{6}-\sqrt{6}-3\sqrt{2}$
=-2$\sqrt{2}$;
(3)∵m=1+$\sqrt{2}$,n=1-$\sqrt{2}$,
∴m-n=(1+$\sqrt{2}$)-(1-$\sqrt{2}$)=2$\sqrt{2}$,mn=(1+$\sqrt{2}$)(1-$\sqrt{2}$)=-1,
∴$\sqrt{{m}^{2}+{n}^{2}-3mn}$
=$\sqrt{(m-n)^{2}-mn}$
=$\sqrt{(2\sqrt{2})^{2}-(-1)}$
=$\sqrt{8+1}$
=3.
点评 本题考查二次根式的化简求值、零指数幂,解题的关键是明确它们的计算方法.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
20.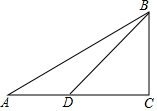 如图,在Rt△ABC中,∠A=30°,CD=CB,则∠ABD的度数是( )
如图,在Rt△ABC中,∠A=30°,CD=CB,则∠ABD的度数是( )
 如图,在Rt△ABC中,∠A=30°,CD=CB,则∠ABD的度数是( )
如图,在Rt△ABC中,∠A=30°,CD=CB,则∠ABD的度数是( )| A. | 15° | B. | 20° | C. | 30° | D. | 60° |
19.以下列各组数为三角形的边长,能构成直角三角形的是( )
| A. | 1,2,3 | B. | 1,1,$\sqrt{2}$ | C. | 2,4,5 | D. | 6,7,8 |
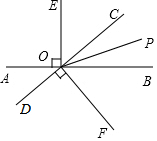 如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD.
如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD.
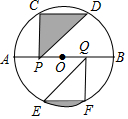 如图,AB是⊙O的直径,点C、D、E、F在⊙O上,且点C、D和点E、F分别是半圆的三等分点,点P、Q在AB上,连接PC、PD、QE、QF,若⊙O的半径为2,则图中阴影部分图形的面积和为$\frac{2}{3}$π(结果保留π).
如图,AB是⊙O的直径,点C、D、E、F在⊙O上,且点C、D和点E、F分别是半圆的三等分点,点P、Q在AB上,连接PC、PD、QE、QF,若⊙O的半径为2,则图中阴影部分图形的面积和为$\frac{2}{3}$π(结果保留π).