Question

4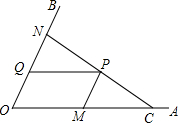．如图，C为∠AOB的边OA上一点，OC=6，N为边OB上异于点O的一动点，P是线段CN上一点，过点P分别作PQ∥OA交OB于点 Q，PM∥OB交OA于点M．
（1）若∠AOB=45，OM=4，OQ=$\sqrt{2}$，求证：CN⊥OB；
（2）当点N在边OB上运动时，四边形OMPQ始终保持为菱形．
①问：$\frac{1}{OM}-\frac{1}{ON}$的值是否发生变化？如果变化，求出其取值范围；如果不变，请说明理由；
②设菱形OMPQ的面积为S₁，△NOC的面积为S₂，求$\frac{{S}_{1}}{{S}_{2}}$的取值范围．

Answer 1

分析 （1）先判断四边形OMPQ为平行四边形，再用锐角三角函数求出∠PCE=45°，即可；
（2）先判断出△NQP∽△NOC，△CPM∽△CNO再得到比例式，求解即可．

解答 解：（1）如图1，

过P作PE⊥OA于E，NF⊥OA，
∵PQ∥OA，PM∥OB，
∴四边形OMPQ为平行四边形，
∴PM=OQ=$\sqrt{2}$，∠PME=∠AOB=45°，
∴PE=PMsin45°=1，ME=1，
∴CE=OC-OM-ME=1，
∴tan∠PCE=$\frac{PE}{CE}$=1，
∴∠PCE=45°，
∴∠CNO=90°，
∴CN⊥OB；
（2）①$\frac{1}{OM}$-$\frac{1}{ON}$的值不发生变化，
理由：设OM=x，ON=y，
∵四边形OMPQ为菱形，
∴OQ=QP=OM=x，NQ=y-x，
∵PQ∥OA，
∴∠NQP=∠O，
∵∠QNP=∠ONC，
∴△NQP∽△NOC，
∴$\frac{OP}{OC}=\frac{NQ}{NO}$，
∴$\frac{x}{6}=\frac{y-x}{y}$，
∴6y-6x=xy，
∴$\frac{1}{x}$-$\frac{1}{y}$=$\frac{1}{6}$，
∴$\frac{1}{OM}$-$\frac{1}{ON}$=$\frac{1}{6}$；
②如图2，

过P作PE⊥OA，过N作NF⊥OA，
∴S₁=OM×PE，S₂=$\frac{1}{2}$OC×NF，
∴$\frac{{S}_{1}}{{S}_{2}}=\frac{xPE}{3NF}$，
∵PM∥OB，
∴∠PMC=∠O∠，
∵∠PCM=∠NCO，
∴△CPM∽△CNO，
∴$\frac{PE}{NF}=\frac{CM}{CO}=\frac{6-x}{6}$，
∴$\frac{{S}_{1}}{{S}_{2}}=\frac{x（6-x）}{18}$，
∵0＜x＜6，
∴0＜$\frac{{S}_{1}}{{S}_{2}}$＜$\frac{1}{2}$．

点评 此题是四边形综合题，主要考查了相似三角形的性质和判定，平行四边形的判定和性质，锐角三角函数的定义，解本题的关键是用锐角三角函数．