题目内容
17.已知三角形三边长分别为6、7、9,则该三角形的面积为2$\sqrt{110}$.分析 作AD⊥BC于D,则∠ADB=∠ADC=90°,由勾股定理得出AB2-BD2=AC2-CD2,设BD=x,则CD=9-x,得出方程,解方程求出BD,再由勾股定理求出AD,即可求出三角形的面积.
解答 解:如图所示: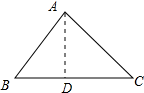
作AD⊥BC于D,则∠ADB=∠ADC=90°,
∴AD2=AB2-BD2,AD2=AC2-CD2,
∴AB2-BD2=AC2-CD2,
设BD=x,则CD=9-x,
∴62-x2=72-(9-x)2,
解得:x=$\frac{34}{9}$,
∴BD=$\frac{34}{9}$,
∴AD2=62-($\frac{34}{9}$)2=$\frac{1760}{81}$,
∴AD=$\frac{4\sqrt{110}}{9}$,
∴△ABC的面积=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×9×$\frac{4\sqrt{110}}{9}$=2$\sqrt{110}$;
故答案为:2$\sqrt{110}$.
点评 本题考查了勾股定理、三角形面积的计算;熟练掌握勾股定理,并能进行推理计算是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.若点A(x1,1)、B(x2,2)、C(x3,-3)在双曲线y=-$\frac{1}{x}$上,则( )
| A. | x1>x2>x3 | B. | x1>x3>x2 | C. | x3>x2>x1 | D. | x3>x1>x2 |
2.下列事件是必然事件的是( )
| A. | 某运动员射击一次击中靶心 | |
| B. | 3个人分成两组,一定有2个人分在一组 | |
| C. | 抛一枚硬币,正面朝上 | |
| D. | 明天一定是晴天 |
 如图,
如图, 如图,在平面直角坐标系中,已知OA=12cm,OB=6cm,点P从点O开始沿OA边向点A以1厘米/秒的速度移动,点Q从点B开始沿BO边向点O以1厘米/秒的速度移动,如果P、Q同时出发,用t秒表示移动的时间(0≤t≤6),那么
如图,在平面直角坐标系中,已知OA=12cm,OB=6cm,点P从点O开始沿OA边向点A以1厘米/秒的速度移动,点Q从点B开始沿BO边向点O以1厘米/秒的速度移动,如果P、Q同时出发,用t秒表示移动的时间(0≤t≤6),那么