题目内容
14. △ABC在平面直角坐标系中的位置如图所示.
△ABC在平面直角坐标系中的位置如图所示.(1)写出△ABC的各顶点坐标A(-2,3),B(-3,2),C(-1,-1);
(2)作出与△ABC关于y轴对称的△A1B1C1;
(3)作出与△ABC关于x轴对称的△A2B2C2;
(4)观察:△A1B1C1和△A2B2C2关于原点对称,若△A1B1C1和△A2B2C2中有任意一组对应点M1,M2,如果点M1的坐标是(x,y),那么点M2的坐标是(-x,-y).
分析 (1)直接利用已知图形得出各点坐标即可;
(2)直接利用关于y轴对称点的性质得出对应点位置进而得出答案;
(3)直接利用关于x轴对称点的性质得出对应点位置进而得出答案;
(4)利用已知图形得出:△A1B1C1和△A2B2C2的位置关系,进而得出利用关于原点对称点的性质得出答案.
解答 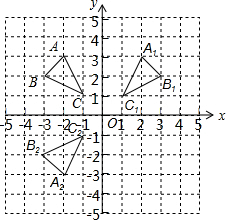 解:(1)如图所示:A(-2,3),B(-3,2),C(-1,-1);
解:(1)如图所示:A(-2,3),B(-3,2),C(-1,-1);
故答案为:-2,3;-3,2,;-1,-1;
(2)如图所示:△A1B1C1,即为所求;
(3)如图所示:△A2B2C2,即为所求;
(4)△A1B1C1和△A2B2C2关于 原点对称,若△A1B1C1和△A2B2C2中有任意一组对应点M1,M2,如果点M1的坐标是(x,y),那么点M2的坐标是(-x,-y).
故答案为:原点,(-x,-y).
点评 此题主要考查了轴对称变换以及关于原点对称点的性质,正确得出对应点位置是解题关键.

练习册系列答案
相关题目
2.下列方程中,没有实数根的是( )
| A. | 2x+3=0 | B. | x2-1=0 | C. | $\frac{1}{x-2}$=$\frac{1-x}{2-x}$-3 | D. | x2+x-1=0 |
3.式子4x2-12x+k是一个完全平方式,则常数k等于( )
| A. | 1.5 | B. | 3 | C. | 2.25 | D. | 9 |
4.某“优质花海专用花籽”的价格为60元/kg,如果一次性购买5kg以上的花籽,超过5kg的部分的花籽的价格打8折.
(1)根据题意,填写下表:
(2)设购买花籽的重量为xkg,付款金额为y元,求y关于x的函数解析式;
(3)若花海园丁李伯伯一次购买该花籽花费了540元,求他购买花籽的重量.
(1)根据题意,填写下表:
| 购买花籽的重量/kg | 3 | 4 | 5 | 6 | … |
| 付款金额/元 | 180 | 240 | 300 | 348 |
(3)若花海园丁李伯伯一次购买该花籽花费了540元,求他购买花籽的重量.
 平行四边形ABCD中,对角线AC、BD交于点O.M为AD中点,连接CM交BD于点N,且ON=1.
平行四边形ABCD中,对角线AC、BD交于点O.M为AD中点,连接CM交BD于点N,且ON=1.