Question

12．如图，抛物线y=ax²+3ax-4a（a≠0）交x轴于A，B（A左B右）两点，点C任线段OA上，且AC：BC=1：4．
（1）求点C的坐标；
（2）过C点作x轴垂线交于抛物线于点D，直线OD的解析式是y=$\frac{4}{3}$x，求抛物线的解析式；
（3）在（2）的条件下，在直线CD上是否存在点P，使得△OPD为等腰三角形？如果存在，请求出满足条件的P点坐标；如果不存在，请说明理由．

Answer 1

分析 （1）令y=0，求出点A，B坐标，计算线段AB长度，根据AC：BC=1：4，可求OC长度为3，即可确定点C坐标；
（2）先求出点D坐标，再代入抛物线解析式求解即可；
（3）分OP=OD，DP=OD，OP=DP，分别求解即可．

解答 解：如图1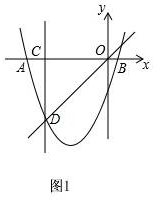

（1）抛物线y=ax²+3ax-4a，
当y=0时，ax²+3ax-4a=0，
解得：x=-4，或x=1，
∴A（-4，0），B（1，0），
∴AC=5，
由AC：BC=1：4，
解得：AC=1，OC=3，
∴C（-3，0），
（2）如图2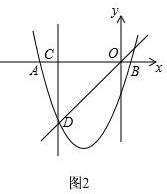

把x=-3代入y=$\frac{4}{3}x$，得，y=-4，
∴D（-3，-4），
代入抛物线y=ax²+3ax-4a得，
a=1，
所以抛物线解析式为：y=x²+3x-4，
（3）如图3

在直角三角形OCD 中，OC=3，CD=4，可求OD=5，cos∠CDO=$\frac{4}{5}$，
当OP=OD时，CP=CD=4，此时点P坐标为（-3，4），
当OD=DP=5时，若点P在点D上方，-4+5=1，点P坐标为（-3，1），
若点P在点D下方，-4-5=-9，点P坐标为（-3，-9），
当OP=DP时，由OD=5，cos∠CDO=$\frac{4}{5}$，可求，DP=$\frac{25}{8}$，
-4+$\frac{25}{8}$=$-\frac{7}{8}$，此时点P坐标为（-3，$-\frac{7}{8}$）．
综上所述，满足条件的P点坐标有：（-3，4），（-3，1），（-3，-9），（-3，$-\frac{7}{8}$）．

点评 此题主要考查二次函数综合问题，会求抛物线与坐标轴的交点，会用点求解析式，会分类讨论等腰三角形进行求点是解题的关键．