题目内容
5.如图1,△ABC中,∠C=90°,BC=3,AC=4,AB=5,将△ABC绕着点B旋转一定的角度,得到△DEB
(1)若点F为AB边上中点,连接EF,则线段EF的范围为0.5≤EF≤5.5
(2)如图2,当△DEB直角顶点E在AB边上时,延长DE,交AC边于点G,请问线段DE、EG、AG具有怎样的数量关系,请写出探索过程.
分析 (1)如图1,利用旋转的性质得BE=BC=3,再根据三角形三边的关系得BE-BF≤EF≤BE+BF(当且仅当B、E、F共线时取等号),从而得到线段EF的范围;
(2)如图2,利用旋转的性质得BE=BC=3,BD=BA=5,DE=AC=4,∠A=∠D,再判断△AGE∽△DEB,然后利用相似比计算出AG、EG,从而可得到线段DE、EG、AG的数量关系.
解答 解:(1)如图1,∵点F为AB边上中点,
∴BF=2.5,
∵△ABC绕着点B旋转一定的角度得到△DE,
∴BE=BC=3,
∵BE-BF≤EF≤BE+BF(当且仅当B、E、F共线时取等号),
∴0.5≤EF≤5.5.
故答案为0.5≤EF≤5.5;
(2)AG+EG=DE.
理由如下:如图2,
∵△ABC绕着点B旋转一定的角度得到△DE,
∴BE=BC=3,BD=BA=5,DE=AC=4,∠A=∠D,
∴AE=AB-BE=2,
∵∠A=∠D,∠AEG=∠BED,
∴△AGE∽△DEB,
∴$\frac{AG}{BD}$=$\frac{EG}{BE}$=$\frac{AE}{DE}$,即$\frac{AG}{5}$=$\frac{EG}{3}$=$\frac{2}{4}$,
∴AG=2.5,EG=1.5,
∴AG+EG=4,
∴AG+EG=DE.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了相似三角形的判定与性质.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
16.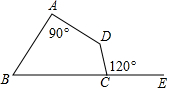 如图,延长四边形ABCD的BC边到E,∠DCE=120°,∠A=90°,∠D=2∠B.那么∠B的度数是( )
如图,延长四边形ABCD的BC边到E,∠DCE=120°,∠A=90°,∠D=2∠B.那么∠B的度数是( )
 如图,延长四边形ABCD的BC边到E,∠DCE=120°,∠A=90°,∠D=2∠B.那么∠B的度数是( )
如图,延长四边形ABCD的BC边到E,∠DCE=120°,∠A=90°,∠D=2∠B.那么∠B的度数是( )| A. | 55° | B. | 60° | C. | 70° | D. | 80° |
13.在下列命题中,真命题的是( )
| A. | 同位角相等 | |
| B. | $\sqrt{4}$=±2 | |
| C. | 三角形的外角等于它相邻的两个内角之和 | |
| D. | 无理数是无限小数 |
10.若a<b<0,则下列各式错误的是( )
| A. | a-2<b-2 | B. | $-\frac{a}{5}<-\frac{b}{5}$ | C. | $\frac{1}{a}>\frac{1}{b}$ | D. | 2a-1<2b-1 |
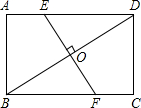 如图矩形ABCD中,AB=3cm,AD=4cm,过对角线BD的中点O作BD的垂直平分线EF,分别交AD、BC于点E、F,则AE的长为$\frac{7}{8}$cm.
如图矩形ABCD中,AB=3cm,AD=4cm,过对角线BD的中点O作BD的垂直平分线EF,分别交AD、BC于点E、F,则AE的长为$\frac{7}{8}$cm.