Question

在等腰Rt△ABC中，∠C=90°，点D是BC上任意一点，连接AD．

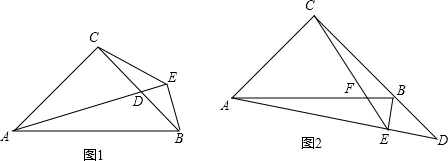
（1）如图1，过点B作BE⊥AD，交射线AD于点E，连接CE，求∠AEC的度数；
（2）如图2，当点D在CB延长线上时，（1）中的条件不变，求∠AEC的度数．

Answer 1

考点：相似三角形的判定与性质,等腰直角三角形

专题：

分析：（1）由已知易证△ACD∽△BED，再证出△CDE∽△ADB，由等腰直角三角形可得∠AEC=∠ABD=45°．
（2）由已知易证△ACD∽△BED，再证出△CDE∽△ADB，由角的关系可得出△AEF∽△CBF，再由等腰直角三角形可得∠AEC=∠ABD=45°．

解答：解：（1）如图1所示，

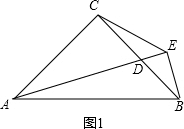
∵∠C=90°，BE⊥AD，
∴∠ACD=∠DEB，且∠ADC=∠BDE，
∴△ACD∽△BED，
∴

DE

CD

=

BD

AD

，即

DE

BD

=

CD

AD

且∠CDE=∠ADB，
∴△CDE∽△ADB，
∴∠AEC=∠ABD，
∵等腰RT△ABC中，∠C=90°，
∴∠AEC=∠ABD=45°．
（2）当点在CB延长线上时，如图2，

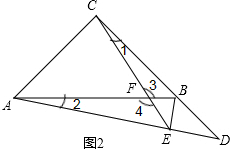
∵∠C=90°，BE⊥AD，
∴∠ACD=∠DEB，且∠ADC=∠BDE，
∴△ACD∽△BED，
∴

DE

CD

=

BD

AD

，即

DE

BD

=

CD

AD

且∠CDE=∠ADB，
∴△CDE∽△ADB，
∴∠1=∠2，
又∵∠3=∠4，
∴△AEF∽△CBF，
∴∠AEC=∠ABD，
∵等腰RT△ABC中，∠C=90°，
∴∠AEC=∠ABD=45°．

点评：本题主要考查了相似三角形的判定与性质及等腰直角三角形，解题的关键是灵活的运用相似三角形的判定与性质．