题目内容

已知方程2x2+kx-2k+1=0的两个实数根的平方和为
29
4
，则k的值为
 
．
考点：根与系数的关系
专题：
分析：根据根与系数的关系求得x1+x2=-
k
2
，x1•x2=-k+
1
2
；然后将其代入x12+x22=（x1+x2）2-4x1x2列出关于k的新方程，通过解新方程即可求得k的值．
解答：解：∵方程2x2+kx-2k+1=0有两个实数根，
∴△=k2-4×2（-2k+1）≥0，
解得k≥6
2
-8或k＜-6
2
-8．
设方程2x2+kx-2k+1=0两个实数根为x1、x2．则
x1+x2=-
k
2
，x1•x2=-k+
1
2
，
∴x12+x22=（x1+x2）2-2x1x2=
k2
4
+2k-1=
29
4
，即k2+8k-33=0，
解得k1=3，k2=-11（不合题意，舍去）．
故答案是：3．
点评：此题主要考查了根与系数的关系，将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法．
练习册系列答案
相关题目
填空
判别式 b2-4ac b2-4ac＜0 b2-4ac＜0
一元二次方程
ax2+bx+c=0		 有两个
 
的实数根		 有两个
 
的实数根
 
实数根
二次函数
y=ax2+bx+c		 图象与x轴有
 

个交点		 图象与x轴有
 

个交点		 图象与x轴有
 

个交点
已知y=
x-2
+
2-x
+3，则xy=
 
．
将一个半径为20cm，圆心角是108度的扇形纸片围成圆锥形纸筒，则需加的底面圆的半径为
 
cm．
请先阅读下列一组内容，然后解答问题：
因为：
1
1×2
=1-
1
2
，
1
2×3
=
1
2
-
1
3
，
1
3×4
=
1
3
-
1
4
…
1
9×10
=
1
9
-
1
10

所以：
1
1×2
+
1
2×3
+
1
3×4
+…+
1
9×10
=(1-
1
2
)+(
1
2
-
1
3
)+(
1
3
-
1
4
)+…+(
1
9
-
1
10
)
=1-
1
2
+
1
2
-
1
3
+
1
3
-
1
4
+…+
1
9
-
1
10
=1-
1
10
=
9
10
问题：
计算：
①
1
1×2
+
1
2×3
+
1
3×4
+…+
1
2004×2005
；
②
1
1×3
+
1
3×5
+
1
5×7
+…+
1
49×51
．
如图，∠MON=45°，点P在射线ON上，OP=4，以P为圆心，r为半径的⊙P与射线OM有两个不同的公共点，则r的取值范围是
 
．
把抛物线y=3x2向右平移4个单位，向下平移3个单位后，得到的抛物线的表达式为
 
．
二元一次方程3a+b=9在正整数范围内的解的个数是（　　）
A、1个B、2个C、3个D、4个
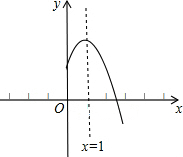二次函数y=ax2+bx+c（a，b，c是常数，a≠0）图象的对称轴是直线x=1，其图象的一部分如图，对于下列说法：
①abc＜0；②a-b+c＜0；③3a+c＜0；④当-1＜x＜3时，y＞0．
其中正确的是（　　）
A、①、②B、①、③
C、①、②、③D、①、②、④

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网