题目内容
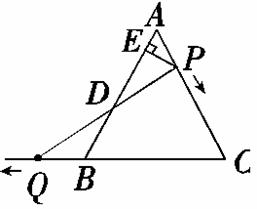
如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一动点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.
(1)若AE=1时,求AP的长;
(2)当∠BQD=30°时,求AP的长;
(3)在运动过程中线段ED的长 是否发生变化?
是否发生变化?
如果不变,求出线段ED的长;
如果发生变化,请说明理由.
(2分)(1)解:
∵ 是等边三角形
是等边三角形
∴∠A=60°
∵
∴∠APE=30°………1分
∵AE=1,∠APE=30°, 
∴AP=2AE=2………1分
(3分)(2)解:
解法一:过 作
作 ,
,
则 是等边三角形,
是等边三角形,
∵ 同时出发,速度相同,即
同时出发,速度相同,即 ,
,
∴ ………1分
………1分
 ∴
∴ ………1分
………1分
∴ ,
,
∵
∴
∴ ………1分
………1分
解法二:∵ 同时同速出发,∴
同时同速出发,∴
设 则
则 ………1分
………1分
在 中,
中,
∴
∴ 即
即 ………1分
………1分
∴
∴ ………1分
………1分
(4分)(3)解:
由(2)知 ,
,
而 是等边三角形,
是等边三角形, ,………1分
,………1分
∵
又
∴ ………2分
………2分
即
∴ 为定值,即
为定值,即 的长不变. ………1分
的长不变. ………1分
(其他解法相应给分)

 B.
B. C.
C. D.
D. 

 2∠A, BC=3cm,则AB= _cm.
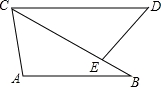
2∠A, BC=3cm,则AB= _cm. 求证:EB=EC.
求证:EB=EC. B.x=1 C.x=2 D.x=3
B.x=1 C.x=2 D.x=3 b=b2﹣a﹣1,例如:7
b=b2﹣a﹣1,例如:7