Question

12．如图，在平面直角坐标系中，A（0，a）、B（b，0），且a，b满足条件$\sqrt{a-6}$+b²-6b+9=0，直线MN：y=kx+4k与x轴交于点M．y轴交于点N．
（1）求直线AB的解析式；
（2）直线MN交直线AB于点C，若S_△MAC=2S_△MBC，求k值．

Answer 1

分析 （1）根据$\sqrt{a-6}$+b²-6b+9=0可得a、b的值，即可知点A、B的坐标，待定系数法即可求得直线AB解析式；
（2）过点C作CP⊥x轴于点P，即可知CP∥OA，根据S_△MAC=2S_△MBC知$\frac{AC}{BC}$=$\frac{OP}{BP}$=2，由OB=3即可得OP的值及点C坐标，将点C坐标代入直线MN：y=kx+4k即可求得k．

解答 解：（1）∵$\sqrt{a-6}$+b²-6b+9=0，即$\sqrt{a-6}$+（b-3）²=0，
∵a=6，b=3，
∴点A（0，6）、点B（3，0），
设直线AB的解析式为：y=mx+n，
∴$\left\{\begin{array}{l}{n=6}\\{3m+n=0}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{m=-2}\\{n=6}\end{array}\right.$，
∴直线AB的解析式为y=-2x+6；

（2）如图，过点C作CP⊥x轴于点P，
∴CP∥OA，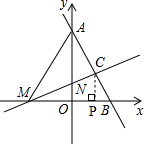

∵S_△MAC=2S_△MBC，
∴AC=2BC，即$\frac{AC}{BC}$=2，
∴$\frac{OP}{BP}$=$\frac{AC}{BC}$=2，
又∵OB=3，
∴OP=2，
在y=-2x+6中，当x=2时，y=2，
即点C（2，2），
将点C（2，2）代入y=kx+4k，得：6k=2，
解得：k=$\frac{1}{3}$．

点评 本题主要考查待定系数法求函数解析式、三角形共高问题、平行线分线段成比例定理等知识点，根据两三角形面积间关系及平行线分线段成比例定理得出点C的坐标是关键．