题目内容
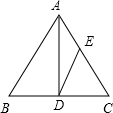
如图，已知AD为△ABC的高，∠B=2∠C，求证：CD=AB+BD．分析：在DC取点E，使DE=BD，连接AE，根据线段垂直平分线求出AB=AE，推出∠B=∠AEB=2∠C=∠C+∠EAC，推出∠C=∠EAC，推出AE=EC=AB，代入即可求出答案．
解答：证明：在DC取点E，使DE=BD，连接AE，
∵AD为△ABC的高，
∴AD⊥BE，
∴AB=AE，
∴∠AEB=∠B，
又∵∠B=2∠C，
∴∠AEB=2∠C，
∵∠AEB=∠C+∠EAC，
∴∠C=∠EAC，
∴AE=EC=AB，
∵CD=DE+EC，BD=DE，
∴CD=AB+BD．
∵AD为△ABC的高，
∴AD⊥BE，
∴AB=AE，
∴∠AEB=∠B，
又∵∠B=2∠C，
∴∠AEB=2∠C，
∵∠AEB=∠C+∠EAC，
∴∠C=∠EAC，
∴AE=EC=AB，
∵CD=DE+EC，BD=DE，
∴CD=AB+BD．
点评：本题考查了线段垂直平分线性质，等腰三角形性质，三角形外角性质的应用，主要考查学生的推理能力．
练习册系列答案
科学实验活动册系列答案
相关题目
如图，已知AD为等腰三角形ABC底边上的高，且tan∠B=| 4 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
如图，已知AD为△ABC的角平分线，DE∥AB交AC于E，如果| AE |
| EC |
| 2 |
| 3 |
| AB |
| AC |
A、
| ||
B、
| ||
C、
| ||
D、
|
如图，已知AD为∠BAC的平分线，且AD=2，AC=
17、如图，已知AD为⊙O的切线，⊙O的直径是AB=2，弦AC=1，则∠CAD=
如图，已知AD为△ABC的角平分线，DE∥AB，如果