题目内容
1.有五张正面分别标有数字-2,0,1,2,3的不透明卡片,它们除数字不同外其他全部相同,现将它们背面朝上,洗匀后从中任取一张,将卡片上的数字记为a,则抽出的数字a使双曲线$y=\frac{a-2}{x}$在第二、四象限,且使抛物线y=ax2+2x-3与x轴有交点的概率为$\frac{1}{5}$.分析 确定使双曲线$y=\frac{a-2}{x}$在第二、四象限,且使抛物线y=ax2+2x-3与x轴有交点的a的值后利用概率公式求解即可.
解答 解:∵双曲线$y=\frac{a-2}{x}$在第二、四象限,
∴a-2<0,
解得:a<2,
∵抛物线y=ax2+2x-3与x轴有交点,
∴22+4×3a≥0,
解得:a≥-$\frac{1}{3}$且a≠0,
∴满足条件的a的值只有1,
∴使双曲线$y=\frac{a-2}{x}$在第二、四象限,且使抛物线y=ax2+2x-3与x轴有交点的概率为$\frac{1}{5}$,
故答案为:$\frac{1}{5}$.
点评 本题考查了概率公式:随机事件A的概率P(A)=事件A可能出现的结果数除以所有可能出现的结果数.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
20.在△ABC中,点D、E分别是边AB、AC上的点,且有$\frac{AD}{DB}$=$\frac{AE}{EC}$=$\frac{1}{2}$,BC=18,那么DE的值为( )
| A. | 3 | B. | 6 | C. | 9 | D. | 12 |
13. 如图,在△ABC中,∠ACB=90°,CD是高,∠A=30°,AB=8,则BD=( )
如图,在△ABC中,∠ACB=90°,CD是高,∠A=30°,AB=8,则BD=( )
 如图,在△ABC中,∠ACB=90°,CD是高,∠A=30°,AB=8,则BD=( )
如图,在△ABC中,∠ACB=90°,CD是高,∠A=30°,AB=8,则BD=( )| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
 一块模板形状如图,按规定,AB,CD的延长线的交角为85°,因交点不在模板上,不便测量,于是工人师傅连结AC,方便地测出了AB,CD的延长线相交所成的角,工人师傅是如何测量的?这块模板符合规定吗?
一块模板形状如图,按规定,AB,CD的延长线的交角为85°,因交点不在模板上,不便测量,于是工人师傅连结AC,方便地测出了AB,CD的延长线相交所成的角,工人师傅是如何测量的?这块模板符合规定吗? 实数a、b、c、m满足:$\frac{a+c}{b}$=$\frac{a+b}{c}$=$\frac{b+c}{a}$=m,那么直线y=mx-$\sqrt{2}$与如图中⊙O的位置关系为相交或相切.
实数a、b、c、m满足:$\frac{a+c}{b}$=$\frac{a+b}{c}$=$\frac{b+c}{a}$=m,那么直线y=mx-$\sqrt{2}$与如图中⊙O的位置关系为相交或相切.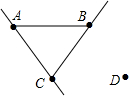 如图所示,按要求画图.
如图所示,按要求画图.