题目内容
7.请从下列三个代数式中任选两个(一个作为分子,一个作为分母)构造一个分式,并化简该分式.a2-1,a2-1,a2-2a+1,然后请你自选一个合理的数代入求值.分析 根据分式的定义即可构造一个分式,然后取一个使得分式有意义的值代入即可.
解答 解:$\frac{{a}^{2}-1}{{a}^{2}-2a+1}$=$\frac{(a+1)(a-1)}{(a-1)^{2}}$=$\frac{a+1}{a-1}$,
当a=2时,原式=$\frac{2+1}{2-1}$=3.
或$\frac{{a}^{2}-2a+1}{{a}^{2}-1}$=$\frac{a-1}{a+1}$,
当a=2时,原式=$\frac{2-1}{2+1}$=$\frac{1}{3}$.
点评 本题考查分式的定义,分式的约分,理解题意是解题的关键,取值时注意使得分式有意义.

练习册系列答案
相关题目
17.一件商品的原价是121元,经过两次降价后的价格为100元,如果每次降价的百分率都是x,根据题意,下面列出的方程正确的是( )
| A. | 121(1+x)=100 | B. | 121(1-x)=100 | C. | 121(1-x)2=100 | D. | 100(1+x)2=121 |
 如图,直线AB、CD相交于点O,∠DOE=∠BOD,OF平分∠AOE,若∠BOD=20°,求∠EOF的度数.
如图,直线AB、CD相交于点O,∠DOE=∠BOD,OF平分∠AOE,若∠BOD=20°,求∠EOF的度数.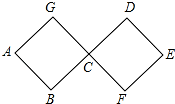 如图,连接在一起的两个正方形的边长都为1cm,一个微型机器人由点A开始按ABCDEFCGA…的顺序沿正方形的边循环移动.
如图,连接在一起的两个正方形的边长都为1cm,一个微型机器人由点A开始按ABCDEFCGA…的顺序沿正方形的边循环移动.