题目内容
12. 如图,已知O为直线AF上一点,OE平分∠AOC,
如图,已知O为直线AF上一点,OE平分∠AOC,(1)若∠AOE=20°,求∠FOC的度数;
(2)若OD平分∠BOC,∠AOB=84°,求∠DOE的度数.
分析 ①利用角平分线的定义求出∠AOC,∠FOC与∠AOC和是180°.
②从图中不难看出∠DOE是由∠AOB与∠BOC半角之和,也就是∠AOB的一半.
解答 解:①∵OE平分∠AOC,∠AOE=20°
∴∠AOC=2∠AOE=40°
∴∠FOC=180°-∠AOC=140°;
②∵OE平分∠AOC,OD平分∠BOC,
∴∠AOE=∠COE=$\frac{1}{2}$∠AOC,∠COD=∠BOD=$\frac{1}{2}$∠BOC,
∴∠DOE=∠COE+∠COD=$\frac{1}{2}$∠AOC+$\frac{1}{2}$∠BOC=$\frac{1}{2}$∠AOB,
已知∠AOB=84°
∴∠DOE=42°.
点评 本题考查了角平分线的定义,解决本题的关键牢记角平分线的定义,注意实际问题中的转化.

练习册系列答案
相关题目
20. 如图所示,C是线段AB的中点,D是线段BC的中点,下列等式不正确的是( )
如图所示,C是线段AB的中点,D是线段BC的中点,下列等式不正确的是( )
 如图所示,C是线段AB的中点,D是线段BC的中点,下列等式不正确的是( )
如图所示,C是线段AB的中点,D是线段BC的中点,下列等式不正确的是( )| A. | CD=BC-DB | B. | CD=AD-AC | C. | $CD=\frac{1}{2}AB-BD$ | D. | $CD=\frac{1}{3}AB$ |
1.从1,2,3,4,5这五个数字任取两个数字,使其乘积为偶数的概率为( )
| A. | $\frac{4}{5}$ | B. | $\frac{7}{10}$ | C. | $\frac{3}{5}$ | D. | $\frac{1}{2}$ |
2. 如果实数a,b,c在数轴上的位置如图所示,那么代数式$\sqrt{{a}^{2}}-|a-b|+\sqrt{{c}^{2}-2ac+{a}^{2}}$可以化简为( )
如果实数a,b,c在数轴上的位置如图所示,那么代数式$\sqrt{{a}^{2}}-|a-b|+\sqrt{{c}^{2}-2ac+{a}^{2}}$可以化简为( )
 如果实数a,b,c在数轴上的位置如图所示,那么代数式$\sqrt{{a}^{2}}-|a-b|+\sqrt{{c}^{2}-2ac+{a}^{2}}$可以化简为( )
如果实数a,b,c在数轴上的位置如图所示,那么代数式$\sqrt{{a}^{2}}-|a-b|+\sqrt{{c}^{2}-2ac+{a}^{2}}$可以化简为( )| A. | -a-b+c | B. | a-b-c | C. | -a-b-c | D. | -a+b-c |
 如图,∠1=∠B,∠2=∠3,∠4=80°,试求∠ADC的度数.
如图,∠1=∠B,∠2=∠3,∠4=80°,试求∠ADC的度数.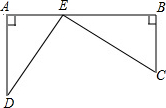 如图,铁路上A、B两站相距25km,C,D为两村庄,且DA⊥AB,CB⊥AB,已知AD=15km,CB=10km,在AB上是否存在一点E,使它到C、D两村庄的距离相等?若存在,求出此时AE的距离;若不存在,请说明理由.
如图,铁路上A、B两站相距25km,C,D为两村庄,且DA⊥AB,CB⊥AB,已知AD=15km,CB=10km,在AB上是否存在一点E,使它到C、D两村庄的距离相等?若存在,求出此时AE的距离;若不存在,请说明理由. 如图,直线AB与CD相交于点O,OE⊥AB,OF⊥CD,OP是∠BOC的平分线.
如图,直线AB与CD相交于点O,OE⊥AB,OF⊥CD,OP是∠BOC的平分线.