题目内容
已知点A(m,n)是一次函数y=-x+3和反比例函数y=
的一个交点,则代数式m2+n2的值为 .
| 1 |
| x |
考点:反比例函数与一次函数的交点问题
专题:
分析:先解两函数式组成的方程组,得出一个一元二次方程,根据根与系数的关系得出m+n=3,mn=1,再根据完全平方公式变形后代入求出即可.
解答:解:方程组
得:
=-x+3,
即x2-3x+1=0,
∵点A(m,n)是一次函数y=-x+3和反比例函数y=
的一个交点,
∴m+n=3,mn=1,
∴m2+n2=(m+n)2-2mn=32-2×1=7,
故答案为:7.
|
| 1 |
| x |
即x2-3x+1=0,
∵点A(m,n)是一次函数y=-x+3和反比例函数y=
| 1 |
| x |
∴m+n=3,mn=1,
∴m2+n2=(m+n)2-2mn=32-2×1=7,
故答案为:7.
点评:本题考查了反比例函数和一次函数的交点问题,一元二次方程的根与系数的关系,完全平方公式的应用,主要考查学生的理解能力和计算能力.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
将5.62×10-4用小数表示为( )
| A、0.000 562 |
| B、0.000 056 2 |
| C、0.005 62 |
| D、0.000 005 62 |
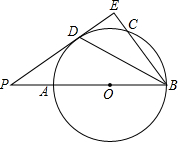 如图,在⊙O中,点P为直径BA延长线上一点,直线PD切⊙O于点D,过点B作BE⊥PD,垂足为E,BE交⊙O于点C,连接BD.
如图,在⊙O中,点P为直径BA延长线上一点,直线PD切⊙O于点D,过点B作BE⊥PD,垂足为E,BE交⊙O于点C,连接BD. 如图,在同心圆中,两圆半径分别是3和1,∠AOB=120°,则阴影部分的面积为
如图,在同心圆中,两圆半径分别是3和1,∠AOB=120°,则阴影部分的面积为