题目内容
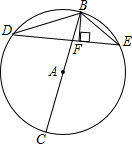如图，BC是⊙A的直径，△DBE的各个顶点在⊙A上，BF⊥DE于点F．求证：BD•BE=BC•BF．考点：相似三角形的判定与性质,圆周角定理
专题：证明题
分析：如图，作辅助线；证明△BDC∽△BFE，得到
=
，进而得到BD•BE=BC•BF，即可解决问题．
| BD |
| BF |
| BC |
| BE |
解答：
证明：如图，连接DC；则∠C=∠E；
∵BC为⊙A的直径，BF⊥DE，
∴∠BDC=∠BFE，
∴△BDC∽△BFE，
∴
=
，
∴BD•BE=BC•BF．
证明：如图，连接DC；则∠C=∠E；∵BC为⊙A的直径，BF⊥DE，
∴∠BDC=∠BFE，
∴△BDC∽△BFE，
∴
| BD |
| BF |
| BC |
| BE |
∴BD•BE=BC•BF．
点评：该题以圆为载体，以圆周角定理及其推论、相似三角形的判定及其性质等几何知识点为考查的核心构造而成；灵活运用圆周角定理及其推论、相似三角形的判定及其性质是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
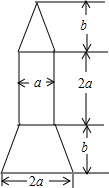2013年6月11日17时18分，神舟十号载人飞船顺利升空，同学们倍受鼓舞，开展了火箭模型的制作比赛，如图为火箭模型的截面图：下面为等腰梯形，中间是长方形，上面是三角形．
根据图填空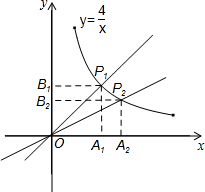
已知：如图，函数y=
如图，已知直线y=ax+b过A（-1，6）与双曲线y=