题目内容
重庆市沙坪坝凯瑞商都购进一批工艺品销售,在试销过程中发现:若按每件200元的价格出售,商场每天可售出该工艺品100件;若每件工艺品降价1元,则每天可多售出该工艺品4件,若这批工艺品进价为每件155元,则每件工艺品降价多少元出售,每天获得的利润最大?获得的最大利润是多少元?
考点:二次函数的应用
专题:销售问题
分析:先根据题意设每件工艺品降价为x元出售,获利y元,则降价x元后可卖出的总件数为(100+4x),每件获得的利润为(200-x-155),此时根据获得的利润=卖出的总件数×每件工艺品获得的利润,列出二次方程,再根据求二次函数最值的方法求解出获得的最大利润即可.
解答:解:设每件工艺品降价x元出售,获利y元,
则根据题意可得:
y=(200-x-155)(100+4x)=4(-x2+20x+1125);
当x=10时,y取得最大值4900元.
即降价10元时,y最大=4900(元).
则根据题意可得:
y=(200-x-155)(100+4x)=4(-x2+20x+1125);
当x=10时,y取得最大值4900元.
即降价10元时,y最大=4900(元).
点评:本题考查的是二次函数在实际生活中的应用,解题的关键是从实际问题中抽象出二次函数模型,比较简单.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
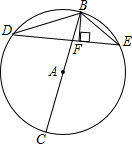 如图,BC是⊙A的直径,△DBE的各个顶点在⊙A上,BF⊥DE于点F.求证:BD•BE=BC•BF.
如图,BC是⊙A的直径,△DBE的各个顶点在⊙A上,BF⊥DE于点F.求证:BD•BE=BC•BF. 如图,在?ABCD中,E、F是对角线BD上的两点,BE=DF,点G、H分别在BA和DC的延长线上,且AG=CH,连接GE、EH、HF、FG.求证:
如图,在?ABCD中,E、F是对角线BD上的两点,BE=DF,点G、H分别在BA和DC的延长线上,且AG=CH,连接GE、EH、HF、FG.求证: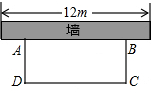 如图,科技小组准备用材料围建一个面积为60m2,墙长12.设AD长x,DC长ym.
如图,科技小组准备用材料围建一个面积为60m2,墙长12.设AD长x,DC长ym. 如图,⊙O的半径OD垂直弦AB,垂足为C,连结AO并延长交⊙O于点E,连结EC.若AB=4
如图,⊙O的半径OD垂直弦AB,垂足为C,连结AO并延长交⊙O于点E,连结EC.若AB=4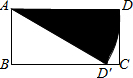 如图,在矩形ABCD中,AB=1,AD=2,将AD边绕点A顺时针旋转,使点D恰好落在BC边上的D′处,则阴影部分的扇形面积为( )
如图,在矩形ABCD中,AB=1,AD=2,将AD边绕点A顺时针旋转,使点D恰好落在BC边上的D′处,则阴影部分的扇形面积为( )