题目内容
14. 如图,一只蚂蚁从长和宽都是4cm,高是6cm的长方体纸盒的A点,沿纸盒爬到B点,它所走的最短路线长10cm.
如图,一只蚂蚁从长和宽都是4cm,高是6cm的长方体纸盒的A点,沿纸盒爬到B点,它所走的最短路线长10cm.
分析 根据”两点之间线段最短”,将点A和点B所在的两个面进行展开,展开为矩形,则AB为矩形的对角线,即蚂蚁所行的最短路线为AB.
解答  解:将点A和点B所在的两个面展开,
解:将点A和点B所在的两个面展开,
①矩形的长和宽分别为4cm和6cm,
故矩形对角线长AB=$\sqrt{{6}^{2}+{8}^{2}}$=10cm;
②矩形的长和宽分别为4cm和10,
故矩形对角线长AB=$\sqrt{{4}^{2}+1{0}^{2}}$=2$\sqrt{34}$cm.
即蚂蚁所行的最短路线长是10cm.
故答案为:10.
点评 本题考查了平面展开-最短路径问题,先根据题意把立体图形展开成平面图形后,再确定两点之间的最短路径.一般情况是两点之间,线段最短.在平面图形上构造直角三角形解决问题,解本题的关键是将点A和点B所在的面展开,运用勾股定理求出矩形的对角线.

练习册系列答案
相关题目
4.7的倒数是( )
| A. | $\frac{1}{7}$ | B. | -$\frac{1}{7}$ | C. | 7 | D. | -7 |
9. 如图,数轴上点M表示的数可能是( )
如图,数轴上点M表示的数可能是( )
 如图,数轴上点M表示的数可能是( )
如图,数轴上点M表示的数可能是( )| A. | 3的算术平方根 | B. | 3的立方根 | C. | 5的算术平方根 | D. | 8的立方根 |
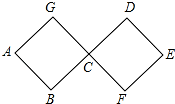 如图,连接在一起的两个正方形的边长都为1cm,一个微型机器人由点A开始按ABCDEFCGA…的顺序沿正方形的边循环移动.
如图,连接在一起的两个正方形的边长都为1cm,一个微型机器人由点A开始按ABCDEFCGA…的顺序沿正方形的边循环移动. 如图,已知∠MAN=120°,AC平分∠MAN,∠ABC+∠ADC=180°,求证:①DC=BC; ②AD+AB=AC.
如图,已知∠MAN=120°,AC平分∠MAN,∠ABC+∠ADC=180°,求证:①DC=BC; ②AD+AB=AC. 如图,阴影部分是由4段以正方形边长的一半为半径的圆弧围成的,这个图形被称作为斯坦因豪斯图形.若图中正方形的边长为a,则阴影部分的面积为$\frac{1}{2}{a^2}$.
如图,阴影部分是由4段以正方形边长的一半为半径的圆弧围成的,这个图形被称作为斯坦因豪斯图形.若图中正方形的边长为a,则阴影部分的面积为$\frac{1}{2}{a^2}$.