题目内容
 已知,在?ABCD中,点M、N分别是AB、CD的中点,AN、CM交DB于P、Q两点,下列结论:①PD=PQ=QB; ②AP=CQ;③CQ=2MQ; ④SADP=
已知,在?ABCD中,点M、N分别是AB、CD的中点,AN、CM交DB于P、Q两点,下列结论:①PD=PQ=QB; ②AP=CQ;③CQ=2MQ; ④SADP=| 1 |
| 4 |
| A、4个 | B、、3个 | C、2个 | D、1个 |
分析:①由于四边形ABCD是?,那么有AB∥CD,利用平行线分线段成比例定理的推论,可证△DPN∽△BPA,从而有DP:BP=1:2(1),同理有BQ:DQ=1:2(2),(1)、(2)联合可求DP=PQ=QB;②根据SAS易证△ADP≌△CBQ,从而有AP=CQ;③由①中知△BQM∽△DQC,利用相似三角形的性质可求CG=2MQ;④由①知P、Q是BD的三等分点,利用同底等高的三角形面积相等可知S△ADP=
S△ABD,而S△ABD=
S?ABCD,易证S△ADP=
S?ABCD.
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
解答:解:①∵四边形ABCD是?,
∴AB∥CD,
∴△DPN∽△BPA,
∴DN:AB=DP:BP,
即DP:BP=1:2(1),
同理有BQ:DQ=1:2(2),
(1)、(2)联合和得:DP=PQ=QB,
故①正确;
②在△ADP和△CBQ中,
∵AD=BC,∠ADP=∠CBQ,DP=BQ,
∴△ADP≌△CBQ,
∴AP=CQ,
故②正确;
③由①中知△BQM∽△DQC,
∴MQ:CQ=1:2,
即CG=2MQ,
故③正确;
④由①知P、Q是BD的三等分点,
∴S△ADP=
S△ABD,
又∵S△ABD=
S?ABCD,
∴S△ADP=
S?ABCD,
故④错误.
故选B.
∴AB∥CD,
∴△DPN∽△BPA,

∴DN:AB=DP:BP,
即DP:BP=1:2(1),
同理有BQ:DQ=1:2(2),
(1)、(2)联合和得:DP=PQ=QB,
故①正确;
②在△ADP和△CBQ中,
∵AD=BC,∠ADP=∠CBQ,DP=BQ,
∴△ADP≌△CBQ,
∴AP=CQ,
故②正确;
③由①中知△BQM∽△DQC,
∴MQ:CQ=1:2,
即CG=2MQ,
故③正确;
④由①知P、Q是BD的三等分点,
∴S△ADP=
| 1 |
| 3 |
又∵S△ABD=
| 1 |
| 2 |
∴S△ADP=
| 1 |
| 6 |
故④错误.
故选B.
点评:本题考查了平行线分线段成比例定理的推论、相似三角形的判定和性质、全等三角形的判定和性质、三角形面积的计算.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 11、如图,已知:在?ABCD中,AE⊥BC交BC于E,AF⊥CD交CD于F,∠EAF=60°,BE=2cm,DF=3cm,则AB=
11、如图,已知:在?ABCD中,AE⊥BC交BC于E,AF⊥CD交CD于F,∠EAF=60°,BE=2cm,DF=3cm,则AB= 已知:在?ABCD中,∠A的角平分线交CD于E,若DE:EC=3:1,AB的长为8,求BC的长.
已知:在?ABCD中,∠A的角平分线交CD于E,若DE:EC=3:1,AB的长为8,求BC的长. 如图,已知:在?ABCD中,E是BC的中点,AE交BD于F,且AE=9,BD=12,AD=10,则?ABCD的面积是
如图,已知:在?ABCD中,E是BC的中点,AE交BD于F,且AE=9,BD=12,AD=10,则?ABCD的面积是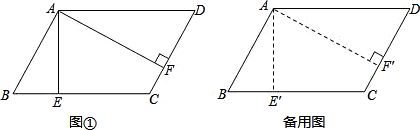 并探究图形中(1)的结论是否依然成立,说明你的理由.
并探究图形中(1)的结论是否依然成立,说明你的理由.