题目内容
11、如图，已知：在?ABCD中，AE⊥BC交BC于E，AF⊥CD交CD于F，∠EAF=60°，BE=2cm，DF=3cm，则AB=4
cm，AD=6
cm．分析：本题可运用四边形内角和定理，先求∠C，在求∠D，∠B．分别在两个直角三角形中，解直角三角形即可．
解答：解：∵AE⊥BC，AF⊥CD，∠EAF=60°，
又由四边形AECF的内角和定理得
∠C+∠AEC+∠AFC+∠EAF=360°，
∴∠C+90°+90°+60°=360°，
∴∠C=120°，∠D=∠B=60°，
∴AD=2DF=6，AB=2BE=4．
故答案为4，6．
又由四边形AECF的内角和定理得
∠C+∠AEC+∠AFC+∠EAF=360°，
∴∠C+90°+90°+60°=360°，
∴∠C=120°，∠D=∠B=60°，
∴AD=2DF=6，AB=2BE=4．
故答案为4，6．
点评：本题结合直角三角形考查了平行四边形的性质，平行四边形的性质有：（1）平行四边形的对边平行且相等．（2）平行四边形的对角相等；（3）平行四边形的对角线互相平分．
练习册系列答案
相关题目
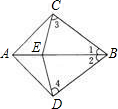
如图，已知：在Rt△ABC中，∠C=90°，E为AB的中点，且DE⊥AB于E，若∠CAD：∠DAB=1﹕2，求∠B的度数．
