题目内容
8.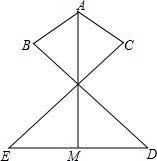 已知如图,AB=AC,∠BAM=∠CAM,CE=BD,M是ED的中点,试说明:AM⊥ED.
已知如图,AB=AC,∠BAM=∠CAM,CE=BD,M是ED的中点,试说明:AM⊥ED.
分析 根据全等三角形的判定与性质,可得BF与CF的关系,根据等式的性质,可得EF与DF的关系,根据等腰三角形的性质,可得答案.
解答 证明:如图: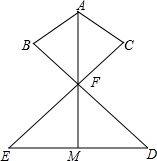
在△ABF和△ACF中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAF=∠CAF}\\{AF=AF}\end{array}\right.$,
∴△ABF≌△ACF(SAS),
∴BF=CF.
∵BD=CE,
∴BD-BF=CE-CF,
即BE=DF.
又∵ME=MD,
∴FM⊥DE,
即AM⊥DE.
点评 本题考查了全等三角形的判定与性质,利用了全等三角形的判定与性质,等腰三角形的性质:顶角的角平分线,底边的中线,底边的高线互相重合.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
19.为了解某市七年级学生的肺活量,从中随机抽样调查了400名学生的肺活量,这项调查中的样本是( )
| A. | 某市八年级学生的肺活量 | B. | 从中抽取的400名学生 | ||
| C. | 从中抽取的400名学生的肺活量 | D. | 400 |
3.下列运算正确的是( )
| A. | a2•a3=a6 | B. | (a2)3=a5 | C. | (-ab2)6=a6b12 | D. | (a+b)2=a2+b2 |
17.一个角的余角是它的3倍,则这个角的度数是( )
| A. | 22.5° | B. | 25° | C. | 30° | D. | 20.5° |
 ,按此规律
,按此规律 =-5.
=-5.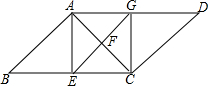 如图,在△ABC中,AB=AC,将△ABC绕点A逆时针方向旋转60°得到△ACD.
如图,在△ABC中,AB=AC,将△ABC绕点A逆时针方向旋转60°得到△ACD.