题目内容
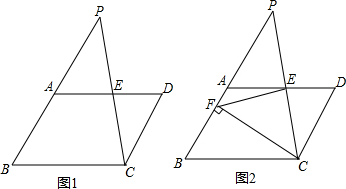
2.如图1,在?ABCD中,AB=2$\sqrt{5}$,tanB=2,点E是AD边的中点,CE的延长线与BA的延长线相交于点P.(1)求证:AP=AB;
(2)点F是线段BP上一点,且CF⊥BP,连接EF;
①若AF=$\frac{1}{2}$AB,直接写出EF的长;
②如图2,若BC=4$\sqrt{5}$,∠FED与∠PFE之间的数量关系满足∠FED=n∠PFE,求n的值.
分析 (1)根据平行四边形的性质可知AE∥BC,根据平行线的性质和点E是AD边的中点,得到答案;
(2)①根据AB=2$\sqrt{5}$,AF=$\frac{1}{2}$AB,求出AF的长和BF的长,根据勾股定理求出PC,根据直角三角形的性质得到答案;
②证明∠FED=3∠PFE,求出n的值.
解答 解:(1)∵四边形ABCD是平行四边形,
∴AE∥BC,
∴$\frac{AE}{BC}$=$\frac{PA}{PB}$,
又∵点E是AD边的中点,
∴PB=2PA,
即AP=AB;
(2)∵AF=$\frac{1}{2}$AB=$\sqrt{5}$,
∴BF=$\sqrt{5}$,
又∵CF⊥BP,tanB=2,
∴FC=2$\sqrt{5}$,
PF=PA+AF=3$\sqrt{5}$,
根据勾股定理,PC=$\sqrt{P{F}^{2}+F{C}^{2}}$=$\sqrt{65}$,
由(1)得,PE=EC,
∵CF⊥BP,PE=EC,
∴EF=$\frac{1}{2}$PC=$\frac{\sqrt{65}}{2}$;
②∵EF=PE=EC,
∴∠P=∠PFE,∠FEC=∠P+∠PFE=2∠PFE,
又∵AP=AE,
∴∠P=∠AEP=∠CED,
∴∠FED=3∠PFE,
∴n=3.
点评 本题考查的是平行四边形的性质、直角三角形的性质和平行线的性质,灵活运用性质进行解答是解题的关键,直角三角形的性质:直角三角形斜边上的中线是斜边的一半.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
5. 如图,BC⊥AE于点C,CD∥AB,∠B=40°,则∠ECD的度数是( )
如图,BC⊥AE于点C,CD∥AB,∠B=40°,则∠ECD的度数是( )
 如图,BC⊥AE于点C,CD∥AB,∠B=40°,则∠ECD的度数是( )
如图,BC⊥AE于点C,CD∥AB,∠B=40°,则∠ECD的度数是( )| A. | 70° | B. | 60° | C. | 50° | D. | 40° |
14. 如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x袖于点M,交y轴于点N,再分别以点M、N为圆心,大于MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2a,b+1),则a与b的数量关系为( )
如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x袖于点M,交y轴于点N,再分别以点M、N为圆心,大于MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2a,b+1),则a与b的数量关系为( )
 如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x袖于点M,交y轴于点N,再分别以点M、N为圆心,大于MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2a,b+1),则a与b的数量关系为( )
如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x袖于点M,交y轴于点N,再分别以点M、N为圆心,大于MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2a,b+1),则a与b的数量关系为( )| A. | a-b | B. | 2a+b=-1 | C. | 2a-b=l | D. | 2a+b=l |
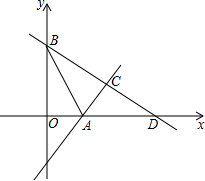 如图,在平面直角坐标系中,点A在x轴的正半轴上,点B在y轴的正半轴上,且线段OA、OB(OA<OB)的长是方程x2-9x+18=0的两根,将
如图,在平面直角坐标系中,点A在x轴的正半轴上,点B在y轴的正半轴上,且线段OA、OB(OA<OB)的长是方程x2-9x+18=0的两根,将