题目内容
14.去分母解关于x的方程$\frac{2}{x-2}$+$\frac{mx}{{x}^{2}-4}$=0得到使分母为0的根,求m的值.分析 先把分式化为整式方程2(x+2)+mx=0,由于原分式方程有增根,则有(x+2)(x-2)=0,得到x=2或-2,即增根为2或-2,然后把x=2或-2代入整式方程即可得到m的值.
解答 解:方程两边乘以(x+2)(x-2),去分母得:2(x+2)+mx=0,
(2+m)x+4=0,
∵分式方程有增根,
∴(x+2)(x-2)=0,得到x=2或-2,
当x=2时,2(2+m)+4=0,解得:m=-3,
当x=-2时,-2(2+m)+4=0,解得:m=-1.
点评 题考查了分式方程的增根:先把分式方程两边乘以最简公分母,把分式方程转化为整式方程,再解整式方程,然后把整式方程的解代入最简公分母中,若其值不为零,则此解为原分式方程的解;若其值为0,则此整式方程的解为原分式方程的增根.

练习册系列答案
相关题目
6.物体自由下落的高度h(m)和下落时间t(s)的关系是:在地球上大约是h=4.9t2,在月球上大约是h=0.8t2.
(1)填写下表并判断物体在哪下落得快?地球
(2)当h=20m时,比较物体在地球上和在月球上自由下落所需要的时间?
(1)填写下表并判断物体在哪下落得快?地球
| t | 0 | 2 | 4 | 6 | 8 | 10 |
| h=4.9t2 | 0 | 19.6 | 78.4 | 176.4 | 313.6 | 490 |
| H=0.8t2 | 0 | 3.2 | 12.8 | 28.8 | 51.2 | 80 |
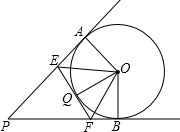 如图所示,PA,PB是⊙O的切线,切点分别是点A,B.点Q为AB上一点.过点Q作⊙O的切线,分别交PA,PB于E,F两点.已知PA=12cm,∠P=56°.
如图所示,PA,PB是⊙O的切线,切点分别是点A,B.点Q为AB上一点.过点Q作⊙O的切线,分别交PA,PB于E,F两点.已知PA=12cm,∠P=56°.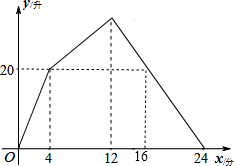 某容器装有一个进水管和三个相同的出水管,从某时刻开始的4分钟内只进水不出水,在随口的8分钟内在进水的同时开放一个出水管出水.每分钟单个进水管和出水管的进、出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分)的关系如图所示
某容器装有一个进水管和三个相同的出水管,从某时刻开始的4分钟内只进水不出水,在随口的8分钟内在进水的同时开放一个出水管出水.每分钟单个进水管和出水管的进、出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分)的关系如图所示