题目内容

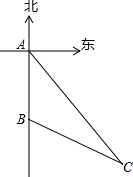某次台风袭击了我国西南部海域．如图，台风来临前，我国海上搜救中心A接到一渔船遇险的报警，于是令位于A的正南方向180海里的救援队B立即施救．已知渔船所处位置C在A的南偏东34°方向，在B的南偏东63°方向，此时离台风来到C处还有12小时，如果救援船每小时行驶20海里，试问能否在台风来到之前赶到C处对其施救？
考点：解直角三角形的应用-方向角问题
专题：
分析：利用已知过点C作CD⊥AB延长线于点D，利用锐角三角函数关系得出BD的长，进而求出BC的长，即可得出答案．
解答：解：过点C作CD⊥AB延长线于点D，
∵∠DAC=34°，∠DBC=63°，
∴设BD=x，则tan63°=
CD
BD
，故CD=BDtan63°=xtan63°，
∴tan34°=
DC
AB+BD
=
xtan63°
180+x
，
解得：x≈94.3，
故cos63°=
BD
BC
=
94.3
CB
，
解得：BC≈207.7，
207.7÷20≈10.4（小时），
答：如果救援船每小时行驶20海里，能在台风来到之前赶到C处对其施救．
点评：此题主要考查了方向角问题的应用，正确使用计算器求出BC的长是解题关键．
练习册系列答案
相关题目
若2a=3b=4c，且abc≠0，则
a+b
c-2b
的值是
 
．
从1-9中挑出4个数字，填入下表，使算式成立，一共有
 
种填法．
在平面直角坐标系中，点P（x，y），其中xy＞0，x＞y，且点P到x轴、y轴的距离分别为6和2，则点P的坐标为（　　）
A、（2，6）
B、（-6，-2）
C、（6，2）
D、（-2，-6）
在△ABC中，AD是角平分线．
（1）求证：
BD
DC
=
AB
AC
；
（2）探究若AD为△ABC外角的平分线，交BC延长线于点D，上面的结论是否成立？说明理由．
如图所示，最外侧大圆的面积是半径为2厘米的小圆面积的几倍？阴影部分的面积是半径为3厘米的圆的面积的多少？
如图，△ABC为等腰直角三角形，∠BAC=90°，在边BC上取点D，使BD=2DC，BE⊥AD交AC于E，垂足为F．求证：AE=EC．
以下四个三角形，与如图的三角形相似的是（　　）
A、
B、
C、
D、
直角三角形两直角边的比是24：7，则周长与最短边的比是（　　）
A、7：1B、8：1
C、25：7D、31：7

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网