题目内容
直角三角形两直角边的比是24：7，则周长与最短边的比是（ ）
| A、7：1 | B、8：1 |
| C、25：7 | D、31：7 |
考点：勾股定理
专题：计算题
分析：根据已知比例式设出两直角边，利用勾股定理表示出斜边，求出周长与最短边之比即可．
解答：解：由直角三角形两直角边的比是24：7，设两直角边分别为24k，7k，
根据勾股定理得：斜边为
=25k，
∴三角形周长为24k+7k+25k=56k，最短边为7k，
则周长与最短边的比是8：1．
故选B
根据勾股定理得：斜边为
| (24k)2+(7k)2 |
∴三角形周长为24k+7k+25k=56k，最短边为7k，
则周长与最短边的比是8：1．
故选B
点评：此题考查了勾股定理，熟练掌握勾股定理是解本题的关键．
练习册系列答案
相关题目
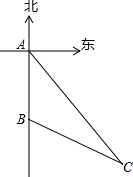某次台风袭击了我国西南部海域．如图，台风来临前，我国海上搜救中心A接到一渔船遇险的报警，于是令位于A的正南方向180海里的救援队B立即施救．已知渔船所处位置C在A的南偏东34°方向，在B的南偏东63°方向，此时离台风来到C处还有12小时，如果救援船每小时行驶20海里，试问能否在台风来到之前赶到C处对其施救？
△ABC中，D为BC边的中点，延长AD至E、延长AB交CE于P，若AD=2DE，求证：AP=3AB．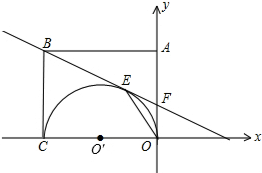
如图，矩形OABC的两边OC、OA分别是x轴和y轴上，过点B的直线切以OC为直径的半圆O′于点E，交y轴于点F，连接OE，且已知C（-6，0），F（0，2）．试求点B的坐标．
已知如图：等边△ABC中，D是AB上一点，∠EDF=60°，则∠AED=（ ）| A、t∠B | B、∠BFD |
| C、∠ADE | D、∠BDF |
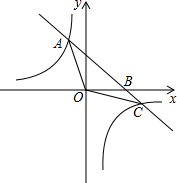如图，已知直线y=-x+4与反比例函数y=