题目内容
在△ABC中，AD是角平分线．（1）求证：
| BD |
| DC |
| AB |
| AC |
（2）探究若AD为△ABC外角的平分线，交BC延长线于点D，上面的结论是否成立？说明理由．
考点：平行线分线段成比例
专题：
分析：（1）如图，作辅助线，证明
=
，进而证明AC=AE，问题即可解决．
（2）如图，作辅助线，证明
=
，进而证明AE=AC，问题即可解决．
| BD |
| CD |
| AB |
| AE |
（2）如图，作辅助线，证明
| BD |
| CD |
| AB |
| AE |
解答：
解：（1）如图1，过点C作CE∥AD交BA的延长线于点E；
则
=
；∠E=∠BAD，∠ACE=∠CAD；
∵AD是角平分线，
∴∠BAD=∠CAD，
∴∠E=∠ACE，
∴AC=AE，
=
．
（2）如图2，过点C作CE∥AD交AB于点E；
则
=
；∠AEC=∠FAD，∠ACE=∠CAD；
∵AD平分∠FAC，
∴∠FAD=∠CAD，
∴∠AEC=∠ACE，
∴AE=AC，
∴
=
．
解：（1）如图1，过点C作CE∥AD交BA的延长线于点E；则
| BD |
| CD |
| AB |
| AE |
∵AD是角平分线，
∴∠BAD=∠CAD，
∴∠E=∠ACE，
∴AC=AE，
| BD |
| DC |
| AB |
| AC |
（2）如图2，过点C作CE∥AD交AB于点E；则
| BD |
| CD |
| AB |
| AE |
∵AD平分∠FAC，
∴∠FAD=∠CAD，
∴∠AEC=∠ACE，
∴AE=AC，
∴
| BD |
| DC |
| AB |
| AC |
点评：该题主要考查了平行线分线段成比例定理及其应用问题；解题的关键是作辅助线，灵活运用有关定理来分析、判断、推理或解答．
练习册系列答案
相关题目
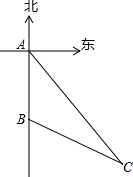某次台风袭击了我国西南部海域．如图，台风来临前，我国海上搜救中心A接到一渔船遇险的报警，于是令位于A的正南方向180海里的救援队B立即施救．已知渔船所处位置C在A的南偏东34°方向，在B的南偏东63°方向，此时离台风来到C处还有12小时，如果救援船每小时行驶20海里，试问能否在台风来到之前赶到C处对其施救？
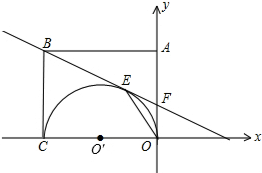如图，矩形OABC的两边OC、OA分别是x轴和y轴上，过点B的直线切以OC为直径的半圆O′于点E，交y轴于点F，连接OE，且已知C（-6，0），F（0，2）．试求点B的坐标．