题目内容
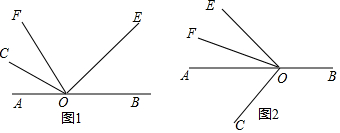
5. 在△ABC中,∠BAC=126°,DE、FG分别为AB、AC的垂直平分线,则∠EAG=72°.
在△ABC中,∠BAC=126°,DE、FG分别为AB、AC的垂直平分线,则∠EAG=72°.
分析 先设∠B=x,∠c=y,由三角形内角和定理可知,∠B+∠C=180°-∠BAC,即x+y=70°,再由DE、GF分别是AB、AC的垂直平分线可知,BE=AE,AG=CG,由等腰三角形的性质可知∠BAE=∠B=x,∠CAG=∠C=y,由∠BAE+∠CAG+∠EAC=∠BAC可列出关于x、y的方程,由∠BAC=110°即可求出答案.
解答 解:∠B=x,∠C=y,则,∠B+∠C=180°-∠BAC,即x+y=54°①,
∵DE、GF分别是AB、AC的垂直平分线,
∴BE=AE,AG=CG,
∴∠BAE=∠B=x,∠CAG=∠C=y,
∵∠BAE+∠CAG+∠EAG=∠BAC,
∴x+y+∠EAG=126°②,
联立①②得,∠EAG=126°-54°=72°.
故答案为:72.
点评 本题考查的是线段垂直平分线的性质,即线段的垂直平分线上的点到线段的两个端点的距离相等.

练习册系列答案
相关题目
15. 如图,点A、B、C、D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C、D、E为顶点的三角形与△ABC相似,则点E的坐标不可能是( )
如图,点A、B、C、D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C、D、E为顶点的三角形与△ABC相似,则点E的坐标不可能是( )
 如图,点A、B、C、D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C、D、E为顶点的三角形与△ABC相似,则点E的坐标不可能是( )
如图,点A、B、C、D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C、D、E为顶点的三角形与△ABC相似,则点E的坐标不可能是( )| A. | (4,2) | B. | (6,0) | C. | (6,3) | D. | (6,5) |
16.下列运算结果正确的是( )
| A. | 5x-x=5 | B. | 2x2+2x3=4x5 | C. | -4b+b=-3b | D. | a2b-ab2=0 |
13. 如图,已知AB∥CD,DE⊥AC,垂足为E,∠A=120°,则∠D的度数为( )
如图,已知AB∥CD,DE⊥AC,垂足为E,∠A=120°,则∠D的度数为( )
 如图,已知AB∥CD,DE⊥AC,垂足为E,∠A=120°,则∠D的度数为( )
如图,已知AB∥CD,DE⊥AC,垂足为E,∠A=120°,则∠D的度数为( )| A. | 30° | B. | 60° | C. | 50° | D. | 40° |
10.用一个放大镜去考查一个角的大小,正确的说法是( )
| A. | 角的度数扩大了 | B. | 角的度数缩小了 | ||
| C. | 角的度数没有变化 | D. | 以上都不对 |
17.“校园足球”已成为灵武市第四张名片,这一新闻获得2400000的点击率,2400000这个数用科学记数法表示,结果正确的是( )
| A. | 0.24×103 | B. | 2.4×106 | C. | 2.4×105 | D. | 24×104 |