题目内容
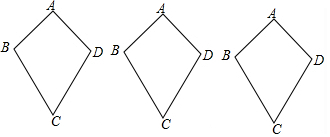
14.定义:两组邻边财应相等的四边形为筝形如图,在筝形ABCD中,AB=AD=2$\sqrt{2}$,BC=CD=6,∠DAB=90°
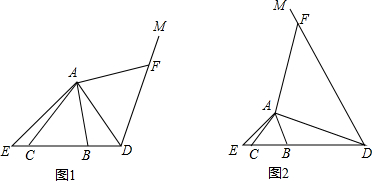
(1)在图1中,作一条直线将筝形ABCD的面积二等分,并说明理由.
(2)在图2中,利用尺规在筝形ABCD中找一点P,连接PB、PD,使折线BPD将筝形ABCD的面积二等分(不写作法).并说明理由.
(3)在筝形ABCD中,是否存在一条过点D的直线将筝形ABCD的面积二等分?若存在,求出该筝形截这条直线所得线段的长的平方;若不存在,请说明理由.
分析 (1)连接AC,判定出△ABC≌△ADC,即可;
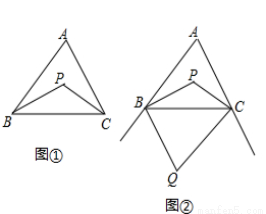
(2)利用三角形的一条直线将三角形分成两个面积相等的三角形即可作出图形;
(3)先求出四边形ABCD的面积,即可得出四边形ABQD的面积,从而求出QM,再用平行线分线段成比例定理求出BM,即可得出DM,最后用勾股定理即可.
解答 解:(1)如图1,
连接 AC,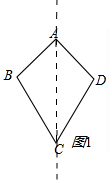
证明:在△ABC 和△ADC 中,$\left\{\begin{array}{l}{AB=AD}\\{CB=CD}\\{AC=AC}\end{array}\right.$,
∴△ABC≌△ADC,
∴S△ABC=S△ADC
∴AC 所在的直线平分筝形的面积.
(2)如图2,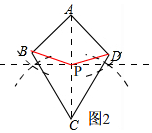
作出AC 的中点P,连接BP、DP,折线B-P-D 将筝形ABCD 面积二等分.
证明:在△ABC 中,
∵P 为AC 边中点,
∴AP=CP,
∴S△APB=S△CPB=$\frac{1}{2}$ S△ABC,
同理:S△APD=S△CPD=$\frac{1}{2}$S△ADC,
∵S△ABC=S△ADC
∴S△APD+S△APB=S△CPB+S△CPD
即四边形ABPD 的面积=四边形BCDP 的面积
∴折线B-P-D将筝形ABCD面积二等分.
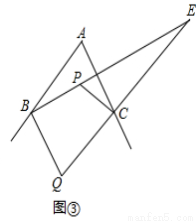
(3)如图3,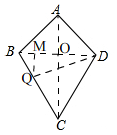
连接BD,AC交于点O.在BC上取一点Q,过Q作QM⊥BD,
∵在△BCO 和△DCO 中,
由(1)知,∠BCA=∠DCA,
在△BCO和△DCO中,$\left\{\begin{array}{l}{BC=DC}\\{∠BCA=∠DCA}\\{OC=OC}\end{array}\right.$
∴△BCO≌△DCO,
∴∠BOC=∠DOC,
∴AC⊥BD,
在Rt△ABD 中,BD=$\sqrt{2}$AB=4,
∴DO=BO=OA=2,
在Rt△BCO 中,OC=$\sqrt{B{C}^{2}-O{B}^{2}}$=4$\sqrt{2}$,
∴S四边形ABCD=S△ABD+S△CBD=$\frac{1}{2}$BD×(AO+CO)=$\frac{1}{2}$×4×(2+4$\sqrt{2}$)=4+8$\sqrt{2}$,
∵在一条过点D的直线将筝形ABCD的面积二等分,
∴S四边形ABQD=$\frac{1}{2}$S四边形ABCD=2+4$\sqrt{2}$,
∵S△ABD=$\frac{1}{2}$×BD×OA=4,
∴S△QBD=$\frac{1}{2}$BD×QM=$\frac{1}{2}$×4×QM=2QM=S四边形ABQD-S△ABD=2+4$\sqrt{2}$-4=4$\sqrt{2}$-2,
∴QM=2$\sqrt{2}$-1,
∵QM∥CO.
∴$\frac{BM}{BO}=\frac{QM}{CO}$,
∴$\frac{BM}{2}=\frac{2\sqrt{2}-1}{4\sqrt{2}}$,
∴BM=$\frac{4-\sqrt{2}}{4}$,
∴DM=BD-BM=$\frac{12+\sqrt{2}}{4}$
在Rt△MQD 中,DQ2=DM2+MQ2=$\frac{145-20\sqrt{2}}{8}$.
点评 此题是四边形综合题,主要考查了等腰三角形的性质,三角形的中线,几何作图,勾股定理,求出四边形ABCD的面积是解本题的关键.

| A. | 都是正数 | B. | 都是负数 | C. | 一正一负 | D. | 符号不能确定 |
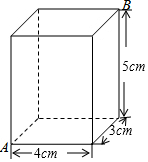 图是一个长、宽、高分别为4cm,3cm,5cm的长方体,一只蚂蚁从顶点A出发,沿长方体的表面爬行至点B,爬行的最短路程是多少?
图是一个长、宽、高分别为4cm,3cm,5cm的长方体,一只蚂蚁从顶点A出发,沿长方体的表面爬行至点B,爬行的最短路程是多少?