题目内容
2.已知关于x的方程x2+(k-4)x-(k-1)=0的两实数根互为相反数,则两根之积为-3.分析 设方程的两根分别为x1,x2,根据根与系数的关系得到x1+x2,=-(k2-4)=0,解得k=±2,然后分别计算△,最后确定k=-2,即可得到结果.
解答 解:设方程的两根分别为x1,x2,
∵x2+(k-4)x-(k-1)=0的两实数根互为相反数,
∴x1+x2=-(k-4)=0,解得k=4,
∴x1x2=1=-(k-1)=-3.
故答案为:-3.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)根与系数的关系:若方程的两根分别为x1,x2,则x1+x2=-$\frac{b}{a}$;x1•x2=$\frac{c}{a}$.也考查了一元二次方程的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
相关题目
7. 如图,在平行四边形ABCD中,F是AD延长线上一点,连接BF交DC与点E,则图中相似三角形共有( )
如图,在平行四边形ABCD中,F是AD延长线上一点,连接BF交DC与点E,则图中相似三角形共有( )
 如图,在平行四边形ABCD中,F是AD延长线上一点,连接BF交DC与点E,则图中相似三角形共有( )
如图,在平行四边形ABCD中,F是AD延长线上一点,连接BF交DC与点E,则图中相似三角形共有( )| A. | 0对 | B. | 1对 | C. | 2对 | D. | 3对 |
12.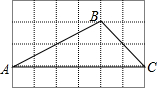 如图,△ABC的顶点都是正方形网格中的格点,则sin∠BAC等于( )
如图,△ABC的顶点都是正方形网格中的格点,则sin∠BAC等于( )
 如图,△ABC的顶点都是正方形网格中的格点,则sin∠BAC等于( )
如图,△ABC的顶点都是正方形网格中的格点,则sin∠BAC等于( )| A. | $\frac{\sqrt{2}}{3}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{\sqrt{10}}{5}$ | D. | $\frac{1}{3}$ |
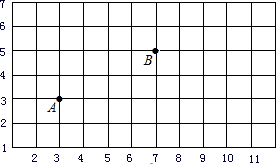 如图,点A用(3,3)表示,点B用(7,5)表示,若用(3,3)→(5,3)→(5,4)→(7,4)→(7,5)表示由A到B的一种走法,并规定从A到B只能向上或向右走,用上述表示法写出另两种走法,并判断这几种走法的路程是否相等.
如图,点A用(3,3)表示,点B用(7,5)表示,若用(3,3)→(5,3)→(5,4)→(7,4)→(7,5)表示由A到B的一种走法,并规定从A到B只能向上或向右走,用上述表示法写出另两种走法,并判断这几种走法的路程是否相等.