Question

2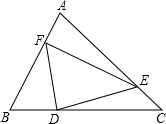．如图，若△DEF面积为a，且BF=2AF，CD=3BD，AE=4CE，则△ABC的面积为（　　）

• A． 3a
• B． $\frac{12}{5}$a
• C． $\frac{4}{3}$a
• D． $\frac{8}{3}$a

Answer 1

分析 如图，连接AD、BE．设△ABC的面积为x．根据S_△ABC-S_△BFD-S_△DEC-S_△AEF=S_△DEF列出方程即可解决问题．

解答 解：如图，连接AD、BE．设△ABC的面积为x．

∵BF=2AF，CD=3BD，AE=4CE，
∴S_△ABD=$\frac{1}{4}$S_△ABC，S_△ADC=$\frac{3}{4}$S_△ABC，S_△ABE=$\frac{4}{5}$S_△ABC，
∴S_△BFD=$\frac{2}{3}$S_△ABD=$\frac{1}{6}$S_△ABC，S_△DEC=$\frac{1}{5}$S_△ADC=$\frac{3}{20}$S_△ABC，S_△AEF=$\frac{1}{3}$S_△ABE=$\frac{4}{15}$S_△ABC，
∴S_△ABC-S_△BFD-S_△DEC-S_△AEF=S_△DEF，
∴x-$\frac{1}{6}$x-$\frac{3}{20}$x-$\frac{4}{15}$x=a，
∴x=$\frac{12}{5}$a．

点评 本题考查三角形的面积，解题的关键是灵活应用异底同高三角形的面积比等于底的比，学会用方程的思想思考问题，属于中考常考题型．