题目内容
1.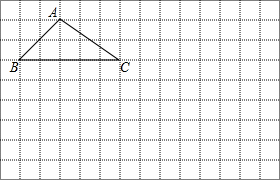 在如图的方格纸中,每个小正方形的边长都是为1.
在如图的方格纸中,每个小正方形的边长都是为1.(1)画出将△ABC向下平移3格得到的△A1B1C1;
(2)画出△A1B1C1以C1为旋转中心,顺时针旋转90°后得到的△A2B2C1;
(3)求△A1B1C1旋转过程中,扫过部分的面积.
分析 (1)利用网格特点和平移的性质画出点AB、C的对应点A1、B1、C1即可;
(2)利用网格特点和旋转的性质画出点A1、B1的对应点A2、B2即可;
(3)△A1B1C1旋转过程中,扫过部分的面积可化为一个扇形和一个三角形,然后根据扇形面积公式和三角形面积公式计算即可.
解答 解:(1)如图,△A1B1C1为所作;
(2)如图,△A2B2C1为所作;
(3)△A1B1C1旋转过程中,扫过部分的面积=S扇形B1C1B2+S△B2C1A2
=$\frac{90•π•{5}^{2}}{360}$+$\frac{1}{2}$×2×5
=$\frac{25}{4}$π+5.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了平移变换.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
11.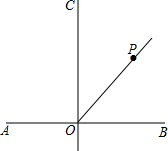 如图,直线AB⊥CD,垂足为O,点P在∠BOC的平分线上,点E在直线AB上,且△EOP是等腰三角形,则这样的点P有( )
如图,直线AB⊥CD,垂足为O,点P在∠BOC的平分线上,点E在直线AB上,且△EOP是等腰三角形,则这样的点P有( )
 如图,直线AB⊥CD,垂足为O,点P在∠BOC的平分线上,点E在直线AB上,且△EOP是等腰三角形,则这样的点P有( )
如图,直线AB⊥CD,垂足为O,点P在∠BOC的平分线上,点E在直线AB上,且△EOP是等腰三角形,则这样的点P有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
9.下列方程组中,哪项的解是$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$( )
| A. | $\left\{\begin{array}{l}{x+y=1}\\{x-y=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=1}\\{x-2y=3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{2x=y}\\{y+x=-3}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{\frac{x}{2}-\frac{y}{6}=1}\\{x+y=3}\end{array}\right.$ |
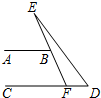 如图,AB∥CD,∠ABE=60°,则∠EFD的度数为120°.
如图,AB∥CD,∠ABE=60°,则∠EFD的度数为120°.