题目内容
3.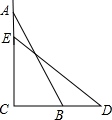 如图,一架梯子AB长2.5m,顶端A靠在墙AC上,这时梯子下端B与墙角C距离1.5m,梯子滑动后停在DE的位置上,如果梯子底端向右滑动的距离与顶端向下滑动的距离相等,求梯子顶端A下滑了多少米.
如图,一架梯子AB长2.5m,顶端A靠在墙AC上,这时梯子下端B与墙角C距离1.5m,梯子滑动后停在DE的位置上,如果梯子底端向右滑动的距离与顶端向下滑动的距离相等,求梯子顶端A下滑了多少米.
分析 首先利用勾股定理计算出AC长,然后设梯子顶端A下滑了x米,则EC=(2-x)m,BD=xm,再利用勾股定理可得(2-x)2+(1.5+x)2=2.52,再解即可.
解答 解:∵AB=2.5m,BC=1.5m,
∴AC=$\sqrt{A{B}^{2}-C{B}^{2}}$=$\sqrt{2.{5}^{2}-1.{5}^{2}}$=2(m),
设梯子顶端A下滑了x米,则EC=(2-x)m,BD=xm,
(2-x)2+(1.5+x)2=2.52,
解得:x1=0(舍去),x2=$\frac{1}{2}$,
答:梯子顶端A下滑了$\frac{1}{2}$米.
点评 此题主要考查了勾股定理的应用,在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型.领会数形结合的思想的应用.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
15.如果甲数除以乙数的商为负数,那么下列说法正确且全面的是( )
| A. | 这两个数的绝对值相等而符号相反 | B. | 甲数为正,乙数为负 | ||
| C. | 甲数为正,乙数不等于0 | D. | 甲、乙两数异号 |
 如图,⊙O的半径OD平分弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=6,CE=5,求CD的长.
如图,⊙O的半径OD平分弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=6,CE=5,求CD的长.