题目内容
19.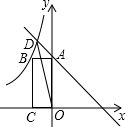 如图,在平面直角坐标系xOy中,直线y=-x+3交y轴于点A,交反比例函数y=$\frac{k}{x}$(k<0)的图象于点D,y=$\frac{k}{x}$(k<0)的图象过矩形OABC的顶点B,矩形OABC的面积为4,连接OD.
如图,在平面直角坐标系xOy中,直线y=-x+3交y轴于点A,交反比例函数y=$\frac{k}{x}$(k<0)的图象于点D,y=$\frac{k}{x}$(k<0)的图象过矩形OABC的顶点B,矩形OABC的面积为4,连接OD.(1)求反比例函数y=$\frac{k}{x}$的表达式;
(2)求△AOD的面积.
分析 (1)根据矩形的面积求出AB,求出反比例函数的解析式;
(2)解方程组求出反比例函数与一次函数的交点,确定点D的坐标,根据三角形的面积公式计算即可.
解答 解:(1)∵矩形OABC的面积为4,双曲线在第二象限,
∴k=-4,
∴反比例函数的表达式为y=-$\frac{4}{x}$;
(2))∵直线y=-x+3交y轴于点A,
∴点A的坐标为(0,3),即OA=3,
解方程组$\left\{\begin{array}{l}{y=-x+3}\\{y=-\frac{4}{x}}\end{array}\right.$,
得$\left\{\begin{array}{l}{{x}_{1}=4}\\{{y}_{1}=-1}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-1}\\{{y}_{2}=4}\end{array}\right.$,
∵点D在第二象限,
∴点D的坐标为(-1,4),
∴△AOD的面积=$\frac{1}{2}$×3×1=$\frac{3}{2}$.
点评 本题考查的是反比例函数与一次函数的交点问题,掌握反比例函数的系数k的几何意义、解方程组求出反比例函数与一次函数的交点是解题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
10.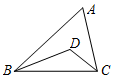 如图,△ABC中,∠A=60°,BD,CD分别是∠ABC,∠ACB的平分线,则∠BDC的度数是( )
如图,△ABC中,∠A=60°,BD,CD分别是∠ABC,∠ACB的平分线,则∠BDC的度数是( )
 如图,△ABC中,∠A=60°,BD,CD分别是∠ABC,∠ACB的平分线,则∠BDC的度数是( )
如图,△ABC中,∠A=60°,BD,CD分别是∠ABC,∠ACB的平分线,则∠BDC的度数是( )| A. | 100° | B. | 110° | C. | 120° | D. | 130° |
7.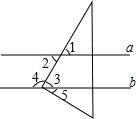 如图,已知直线a∥b,现将一直角三角板的直角顶点放在直线b上,若∠3=50°,则下列结论错误的是( )
如图,已知直线a∥b,现将一直角三角板的直角顶点放在直线b上,若∠3=50°,则下列结论错误的是( )
 如图,已知直线a∥b,现将一直角三角板的直角顶点放在直线b上,若∠3=50°,则下列结论错误的是( )
如图,已知直线a∥b,现将一直角三角板的直角顶点放在直线b上,若∠3=50°,则下列结论错误的是( )| A. | ∠1=50° | B. | ∠2=50° | C. | ∠4=130° | D. | ∠5=30° |
4.下列计算正确的是( )
| A. | 3a-2a=a | B. | $\sqrt{2}+\sqrt{5}$=$\sqrt{7}$ | C. | (2a)3=2a3 | D. | a6÷a3=a2 |
11.某同学家长应邀参加孩子就读中学的开放日活动,他打算上午随机听一节孩子所在1班的课,下表是他拿到的当天上午1班的课表,如果每一节课被听的机会均等,那么他听数学课的概率是$\frac{1}{4}$.
| 班级 节次 | 1班 |
| 第1节 | 语文 |
| 第2节 | 英语 |
| 第3节 | 数学 |
| 第4节 | 音乐 |
8.6的相反数是( )
| A. | -6 | B. | $\frac{1}{6}$ | C. | 6 | D. | ±6 |