题目内容
3. 已知一次函数y=2x-k与反比例函数y=$\frac{k+2}{x}$的图象相交于A、B,其中A的横坐标为3.
已知一次函数y=2x-k与反比例函数y=$\frac{k+2}{x}$的图象相交于A、B,其中A的横坐标为3.(1)求A、B两点的坐标;
(2)若直线AB上有一点P,使得△APO∽△AOB,求P坐标.
分析 (1)首先把A的横坐标为3代入两个函数的解析式中,然后就可以确定k的值,进而得出两个函数的关系式;
(2)利用两个函数的解析式组成方程组,解方程组就可以得到A,B两点的坐标;根据AB两点的坐标得出OA2及AB的长,再由△APO∽△AOB得出$\frac{AP}{OA}$=$\frac{OA}{AB}$,故可得出AP的长,因为点P在直线y=2x-4上,所以设P(x,2x-4),根据两点间的距离公式即可得出AP的表达式,得出x的值,进而得出结论.
解答 解:(1)∵一次函数y=2x-k与反比例函数y=$\frac{k+2}{x}$的图象相交于A和B两点,其中有一个交点A的横坐标为3,
∴$\left\{\begin{array}{l}{y=6-k}\\{y=\frac{k+2}{3}}\end{array}\right.$,
解得k=4.
∴一次函数的解析式为:y=2x-4;反比例函数的关系式为:y=$\frac{6}{x}$;
(2)解$\left\{\begin{array}{l}{y=2x-4}\\{y=\frac{6}{x}}\end{array}\right.$得$\left\{\begin{array}{l}{{x}_{1}=3}\\{{y}_{1}=2}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-1}\\{{y}_{2}=-6}\end{array}\right.$,
∴A(3,2),B(-1,-6);
∴OA2=32+22=13,AB=$\sqrt{(3+1)^{2}+(2+6)^{2}}$=4$\sqrt{5}$,
∵△APO∽△AOB,
∴$\frac{AP}{OA}$=$\frac{OA}{AB}$,
∴OA2=AP•AB,即13=AP•4$\sqrt{5}$,
解得AP=$\frac{13\sqrt{5}}{20}$,
∵点P在直线y=2x-4上,
∴设P(x,2x-4),
∴AP=$\sqrt{(3-x)^{2}+(2-2x+4)^{2}}$,
解得x=3±$\sqrt{42}$,
∴P点坐标为(3+$\sqrt{42}$,2+2$\sqrt{42}$)或(3-$\sqrt{42}$,6-2$\sqrt{42}$).
点评 本题考查的是反比例函数综合题,熟知反比例函数图象上点的坐标特点及两点间的距离公式是解答此题的关键.

 名校通行证有效作业系列答案
名校通行证有效作业系列答案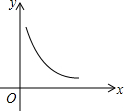 如图中的曲线是反比例函数y=$\frac{m+5}{x}$图象的一支,则m的取值范围是( )
如图中的曲线是反比例函数y=$\frac{m+5}{x}$图象的一支,则m的取值范围是( )| A. | m>-5 | B. | 0<m<5 | C. | -5<m<0 | D. | m<-5 |
 如图,AB为⊙O的直径,C为⊙O外一点,过点C作⊙O的切线,切点为B,连接AC交⊙O于点D,∠C=40°,点E在AB左侧的半圆上运动(不与A、B重合),则∠AED的大小是( )
如图,AB为⊙O的直径,C为⊙O外一点,过点C作⊙O的切线,切点为B,连接AC交⊙O于点D,∠C=40°,点E在AB左侧的半圆上运动(不与A、B重合),则∠AED的大小是( )| A. | 20° | B. | 40° | C. | 50° | D. | 80° |
| 比赛项目 | 演讲 | 书法 | 作文 | 手抄报 | 小品 | 漫画 |
| 参赛人数(人) | 36 | 75 | 90 | 60 | 24 | 15 |
| 比例(%) | 12 | 25 | 30 | 20 | 8 | 5 |
(1)请补充完成统计表;
(2)本次参加比赛的总人数是300人,本次比赛项目的众数是作文.
(3)根据上述数据,你可以获得什么信息.
 B.
B.  C.
C.  D.
D. 
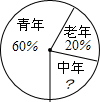 2015年1月份,某区体委组织“迎新春长跑活动”,现将报名的男选手分成:青年组、中年组、老年组,各组人数所占比例如图所示,已知青年组120人,则中年组的人数是40.
2015年1月份,某区体委组织“迎新春长跑活动”,现将报名的男选手分成:青年组、中年组、老年组,各组人数所占比例如图所示,已知青年组120人,则中年组的人数是40.