题目内容
16.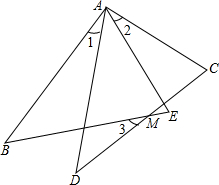 如图所示,AB=AD,AC=AE,∠1=∠2,猜想∠1与∠3的大小关系,并说明你猜想的正确性.
如图所示,AB=AD,AC=AE,∠1=∠2,猜想∠1与∠3的大小关系,并说明你猜想的正确性.
分析 首先证得△ABE≌△ADC,利用全等三角形的性质可得∠B=∠D,由三角形的内角和定理可得∠1=∠3.
解答 解:猜想:∠1=∠3,
∵∠1=∠2,
∴∠1+∠DAE=∠2+∠DAE,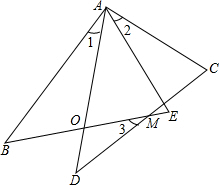
即∠BAE=∠DAC,
在△BAE与△DAC中,
$\left\{\begin{array}{l}{AB=AD}\\{∠BAE=∠DAC}\\{AE=AC}\end{array}\right.$,
∴△BAE≌△DAC(SAS),
∴∠B=∠D,
∵∠AOB=∠DOM,∠1=180°-∠B-∠AOB,∠3=180°-∠D-∠DOM,
∴∠1=∠3.
点评 本题主要考查了全等三角形的性质及判定定理,利用全等三角形的性质得出∠B=∠D是解答此题的关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
5.$\sqrt{64}$的算术平方根是( )
| A. | 2$\sqrt{2}$ | B. | 8 | C. | ±8 | D. | $±2\sqrt{2}$ |
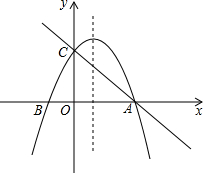 如图,已知抛物线y=-ax2+2ax+3a(a≠0)与x轴交于A、B两点,与y轴交于点C.
如图,已知抛物线y=-ax2+2ax+3a(a≠0)与x轴交于A、B两点,与y轴交于点C. 如图,在△ABC中,∠C=90°,∠B=30°,D为AB上一点,DE⊥BC于E.若BE=AC,DE+BC=3,求BD的长.
如图,在△ABC中,∠C=90°,∠B=30°,D为AB上一点,DE⊥BC于E.若BE=AC,DE+BC=3,求BD的长. 如图,Rt△ABC中,∠ACB=90°,AC=BC,D为AC边上一动点,以BD为边向上作正方形BDEF,O是正方形的对称中心,直线CO分别交BD,EF于点M,N,求证:
如图,Rt△ABC中,∠ACB=90°,AC=BC,D为AC边上一动点,以BD为边向上作正方形BDEF,O是正方形的对称中心,直线CO分别交BD,EF于点M,N,求证: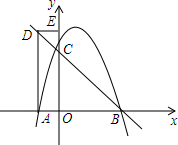 如图,抛物线y=-$\frac{1}{2}{x}^{2}+2x+\frac{5}{2}$与x轴交于点A和点B(A点在B点左侧),与y轴交于点C.
如图,抛物线y=-$\frac{1}{2}{x}^{2}+2x+\frac{5}{2}$与x轴交于点A和点B(A点在B点左侧),与y轴交于点C.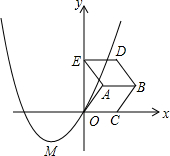 如图,在平面直角坐标系中,过原点的抛物线的顶点M的坐标为(-1,-1),点A的坐标为(1,1),以OA为边的菱形OABC的顶点C在x轴的正半轴上,把菱形OABC沿AB向上翻折得到菱形ABDE.
如图,在平面直角坐标系中,过原点的抛物线的顶点M的坐标为(-1,-1),点A的坐标为(1,1),以OA为边的菱形OABC的顶点C在x轴的正半轴上,把菱形OABC沿AB向上翻折得到菱形ABDE.