题目内容
6．
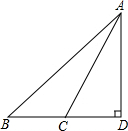如图，Rt△ABC中，∠D=90°，∠B=45°，∠ACD=60°，BC=10cm，求AD的长．
分析 由题意可知△ABD为等腰直角三角形，设AD=BD=xcm，则CD=（x-10）cm，由含30°直角三角形的性质可知：AC=（2x-20）cm，最后在△ACD中依据勾股定理列方程求解即可．
解答 解：∵∠D=90°，∠B=45°，
∴AD=BD．
∵∠D=90°，ACD=60°，
∴∠CAD=30°．
∴AC=2CD．
设AD=BD=xcm，则CD=（x-10）cm，AC=（2x-20）cm．
在Rt△ACD中，由勾股定理得：CD2+AD2=AC2，即（x-10）2+x2=（2x-20）2．
解得：x=5$\sqrt{3}+15$（负值已舍去）．
∴AD=5$\sqrt{3}+15$．
点评 本题主要考查的值勾股定理、含30度直角三角形的性质、等腰三角形的性质，根据题意列出关于x的方程是解题的关键．
练习册系列答案
相关题目
如图，在△ABC中，∠C=90°，∠B=30°，D为AB上一点，DE⊥BC于E．若BE=AC，DE+BC=3，求BD的长．
如图，Rt△ABC中，∠ACB=90°，AC=BC，D为AC边上一动点，以BD为边向上作正方形BDEF，O是正方形的对称中心，直线CO分别交BD，EF于点M，N，求证：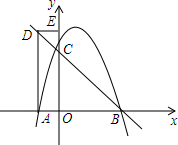
如图，抛物线y=-$\frac{1}{2}{x}^{2}+2x+\frac{5}{2}$与x轴交于点A和点B（A点在B点左侧），与y轴交于点C．