题目内容
4.对于抛物线y=-$\frac{1}{3}$(x-5)2+3,下列说法正确的是( )| A. | 开口向上 | B. | 顶点坐标(-5,3) | ||
| C. | 与y轴的交点坐标是(0,3) | D. | 当x>5时,y随x的增大而减小 |
分析 根据抛物线的解析式,由a的值可得到开口方向,由顶点式可以得到顶点坐标,令x=0代入解析式可得y的值,从而得到与y轴的交点,根据开口方向和对称轴,可知在对称轴左侧与右侧的单调性.
解答 解:∵抛物线y=-$\frac{1}{3}$(x-5)2+3,
∴a=-$-\frac{1}{3}$<0,抛物线的开口向下,故选项A错误;
顶点坐标是(5,3),故选项B错误;
x=0时,y=-$\frac{16}{3}$,故选项C错误;
a=-$-\frac{1}{3}$<0,抛物线的开口向下,对称轴是x=5,当x>5时,y随x的增大而减小,故选项D正确;
故选D.
点评 本题考查二次函数的性质,解题的关键是根据二次函数的解析式可以得到开口方向、对称轴、顶点坐标和单调性.

练习册系列答案
相关题目
12.下列数中不是不等式2x-1>0的解的是( )
| A. | 1 | B. | 0 | C. | 2 | D. | 3 |
9. 一个广告公司制作广告的收费标准是:以面积为单位,在不超过规定面积a(m2)的范围内,每张广告收费100元,若超过am2,则除了要交这100元的基本广告费以外,超过部分还要按每平方米5a元缴费.如表是该公司对两家用户广告的面积及相应收费情况的记载:
一个广告公司制作广告的收费标准是:以面积为单位,在不超过规定面积a(m2)的范围内,每张广告收费100元,若超过am2,则除了要交这100元的基本广告费以外,超过部分还要按每平方米5a元缴费.如表是该公司对两家用户广告的面积及相应收费情况的记载:
红星公司要制作一张大型公益广告,其材料形状是矩形ABCD,如果它的四周是空白,并且四周各空0.5m,空白部分不收广告费,中间的矩形EFGH部分才是广告面积,若矩形ABCD的长宽之比为3:2,并且红星公司只能支出11040元的广告费
(1)求a的值;
(2)求矩形ABCD的长和宽各是多少?(参考数据:1152=13225,232=529)
 一个广告公司制作广告的收费标准是:以面积为单位,在不超过规定面积a(m2)的范围内,每张广告收费100元,若超过am2,则除了要交这100元的基本广告费以外,超过部分还要按每平方米5a元缴费.如表是该公司对两家用户广告的面积及相应收费情况的记载:
一个广告公司制作广告的收费标准是:以面积为单位,在不超过规定面积a(m2)的范围内,每张广告收费100元,若超过am2,则除了要交这100元的基本广告费以外,超过部分还要按每平方米5a元缴费.如表是该公司对两家用户广告的面积及相应收费情况的记载:| 单位 | 广告的面积(m2) | 收费金额(元) |
| 烟草公司 | 6 | 140 |
| 食品公司 | 3 | 100 |
(1)求a的值;
(2)求矩形ABCD的长和宽各是多少?(参考数据:1152=13225,232=529)
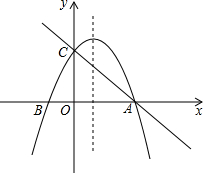 如图,已知抛物线y=-ax2+2ax+3a(a≠0)与x轴交于A、B两点,与y轴交于点C.
如图,已知抛物线y=-ax2+2ax+3a(a≠0)与x轴交于A、B两点,与y轴交于点C. 如图,在△ABC中,∠C=90°,∠B=30°,D为AB上一点,DE⊥BC于E.若BE=AC,DE+BC=3,求BD的长.
如图,在△ABC中,∠C=90°,∠B=30°,D为AB上一点,DE⊥BC于E.若BE=AC,DE+BC=3,求BD的长.