题目内容
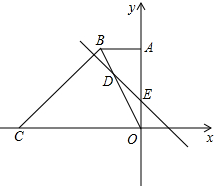 如图,在平面直角坐标系中,直角梯形OABC的边OC、OA分别与x轴、y轴重合,AB∥OC,∠AOC=90°,∠BCO=45°,BC=6,点C的坐标为(-9,0).
如图,在平面直角坐标系中,直角梯形OABC的边OC、OA分别与x轴、y轴重合,AB∥OC,∠AOC=90°,∠BCO=45°,BC=6,点C的坐标为(-9,0).(1)求点B的坐标;
(2)若直线DE交梯形对角线BO于点D,交y轴于点E,且OE=2,OD=2BD,求直线DE的解析式;
(3)若点P是(2)中直线DE上的一个动点,是否存在点P,使以O、E、P为顶点的三角形是等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
考点:一次函数综合题
专题:
分析:(1)根据勾股定理,可得BF、CF,根据线段的和差,可得B点坐标;
(2)根据相似三角形的判定与性质,可得OG、OG的长,根据待定系数法,可得直线的解析式;
(3)分类讨论:OE=OP,OE=EP,OP=EP,先由点在直线上,可设出P点坐标,根据线段的距离相等,可得方程,根据解方程,可得答案.
(2)根据相似三角形的判定与性质,可得OG、OG的长,根据待定系数法,可得直线的解析式;
(3)分类讨论:OE=OP,OE=EP,OP=EP,先由点在直线上,可设出P点坐标,根据线段的距离相等,可得方程,根据解方程,可得答案.
解答:解:(1)如图1:作BF⊥CO,

∵∠BCO=45°,BC=6,
∴CF=BF=3
,
∴OF=OC-CF=9-3
,
∴B点坐标为(3
-9,3
);
(2)如图2:作DG⊥OC与G.
 ,
,
∵DG∥BF,
∴△ODG∽△OBF,
∴
=
=
.∬
∵OD=2BD,
∴
=
=
=
.
OG=
(3
-9)=2
-6,
DG=
×3
=2
∴点D坐标为(2
-6,2
),
∵OE=2,
∴E点坐标为(0,2),
设直线DE解析式为y=kx+b,
代入D,E得:
,
解得
.
直线DE解析式为y=
x+2;
(3)设P(a,
a+2),
①当OE=OP时,即OE2=OP2,22+(
a+2)2=22=4,化简,得
a+2=0,
解得a=2+4
,
a+2=0,即P1(2+4
,0);
②当OE=EP时,OE2=EP2,a2+(
a+2-2)2=22=4,化简,得
a2=2,
解得a=±
,
当a=
时,
a+2=
,
P2(
,
)
当a=-
时,
a+2=
,
P3(-
,
)
③当OP=EP时,即0P2=EP2,a2+(
a+2-2)2=a2+(
a+2)2,
化简,得
a=0,解得a=0
a+2=2,P(0,2)与E点重合,不能与O、P、E为顶点无法形成三角形,P(0,2)(不符合题意的要舍去),
综上所述:P1(2+4
,0);P2(
,
);P3(-
,
).

∵∠BCO=45°,BC=6,
∴CF=BF=3
| 2 |
∴OF=OC-CF=9-3
| 2 |
∴B点坐标为(3
| 2 |
| 2 |
(2)如图2:作DG⊥OC与G.
 ,
,∵DG∥BF,
∴△ODG∽△OBF,
∴
| OG |
| OF |
| DG |
| BF |
| OD |
| OB |
∵OD=2BD,
∴
| OG |
| OF |
| DG |
| BF |
| OD |
| OB |
| 2 |
| 3 |
OG=
| 2 |
| 3 |
| 2 |
| 2 |
DG=
| 2 |
| 3 |
| 2 |
| 2 |
∴点D坐标为(2
| 2 |
| 2 |
∵OE=2,
∴E点坐标为(0,2),
设直线DE解析式为y=kx+b,
代入D,E得:
|
解得
|
直线DE解析式为y=
1-2
| ||
| 7 |
(3)设P(a,
1-2
| ||
| 7 |
①当OE=OP时,即OE2=OP2,22+(
1-2
| ||
| 7 |
1-2
| ||
| 7 |
解得a=2+4
| 2 |
1-2
| ||
| 7 |
| 2 |
②当OE=EP时,OE2=EP2,a2+(
1-2
| ||
| 7 |
29-2
| ||
| 49 |
解得a=±
| 7 |
| 833 |
49964+2332
|
当a=
| 7 |
| 833 |
49964+2332
|
1-2
| ||
| 7 |
(2-4
| ||||||
| 833 |
P2(
| 7 |
| 833 |
49964+2332
|
(2-4
| ||||||
| 833 |
当a=-
| 7 |
| 833 |
49964+2332
|
1-2
| ||
| 7 |
(4
| ||||||
| 833 |
P3(-
| 7 |
| 833 |
49964+2332
|
(4
| ||||||
| 833 |
③当OP=EP时,即0P2=EP2,a2+(
1-2
| ||
| 7 |
1-2
| ||
| 7 |
化简,得
1-2
| ||
| 7 |
1-2
| ||
| 7 |
综上所述:P1(2+4
| 2 |
| 7 |
| 833 |
49964+2332
|
(2-4
| ||||||
| 833 |
| 7 |
| 833 |
49964+2332
|
(4
| ||||||
| 833 |
点评:本题考查了一次函数的综合题,利用了勾股定理,待定系数法求函数解析式,等腰三角形的定义,计算量大,需认真计算.

练习册系列答案
相关题目
 一个长为10m的梯子斜靠在墙上,梯子的底端距墙角6m.
一个长为10m的梯子斜靠在墙上,梯子的底端距墙角6m.