题目内容
若某直角三角形的两条直角边长分别为
cm,
cm,则这个直角三角形的斜边长为多少,面积为多少,斜边上的高为多少cm.
| 6 |
| 17 |
考点:勾股定理
专题:
分析:直接利用勾股定理得出斜边长,再利用直角三角形面积公式得出答案.
解答:解:∵某直角三角形的两条直角边长分别为
cm,
cm,
∴这个直角三角形的斜边长为:
=
(cm),
面积为:
×
×
=
(cm2),
斜边上的高为:
=
(cm),
答:这个直角三角形的斜边长为
cm,面积为
cm2,斜边上的高为
cm.
| 6 |
| 17 |
∴这个直角三角形的斜边长为:
| 6+17 |
| 23 |
面积为:
| 1 |
| 2 |
| 6 |
| 17 |
| ||
| 2 |
斜边上的高为:
| ||||
|
| ||
| 23 |
答:这个直角三角形的斜边长为
| 23 |
| ||
| 2 |
| ||
| 23 |
点评:此题主要考查了勾股定理以及三角形面积,利用面积公式得出斜边上的高是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
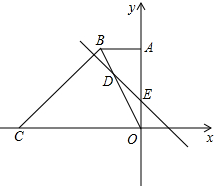 如图,在平面直角坐标系中,直角梯形OABC的边OC、OA分别与x轴、y轴重合,AB∥OC,∠AOC=90°,∠BCO=45°,BC=6,点C的坐标为(-9,0).
如图,在平面直角坐标系中,直角梯形OABC的边OC、OA分别与x轴、y轴重合,AB∥OC,∠AOC=90°,∠BCO=45°,BC=6,点C的坐标为(-9,0).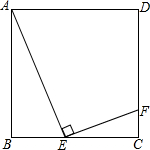 如图,已知边长为1的正方形ABCD,在BC边上有一动点E,连接AE,作EF⊥AE,交CD边于点F.
如图,已知边长为1的正方形ABCD,在BC边上有一动点E,连接AE,作EF⊥AE,交CD边于点F.