题目内容
 一个长为10m的梯子斜靠在墙上,梯子的底端距墙角6m.
一个长为10m的梯子斜靠在墙上,梯子的底端距墙角6m.(1)若梯子的顶端下滑1m,求梯子的底端水平滑动多少米?
(2)若梯子的底端水平向外滑动1m,梯子的顶端向下滑动多少米?
(3)如果梯子顶端向下滑动的距离等于底端向外滑动的距离,那么滑动的距离是多少米?
考点:勾股定理的应用
专题:
分析:(1)先根据勾股定理求出AC的长,进而可得出CE的长;
(2)根据梯子的底端水平向外滑动1m得出CE的长,根据勾股定理求出CD的长,进而可得出结论;
(3)设AD=BE=x,再根据勾股定理即可得出结论.
(2)根据梯子的底端水平向外滑动1m得出CE的长,根据勾股定理求出CD的长,进而可得出结论;
(3)设AD=BE=x,再根据勾股定理即可得出结论.
解答:解:(1)∵△ABC中,AB=10m,BC=6m,
∴AC=
=8(m).
∵梯子的顶端下滑1m,
∴AD=1m,
∴CD=8-1=7(m),
∴CE=
=
=
,
∴BE=CE-BC=(
-6)m.
答:梯子的底端水平滑动(
-6)米;
(2)∵梯子的底端水平向外滑动1m,
∴CE=BC+BE=6+1=7,
∴CD=
=
=
,
∴AD=AC-CD=(10-
)m.
答:梯子的顶端向下滑动(10-
)米;
(3)∵梯子顶端向下滑动的距离等于底端向外滑动的距离,
∴设AD=BE=x,则BC2+AC2=CD2+CE2,即62+82=(8-x)2+(6+x)2,解得x=2(m).
答:滑动的距离是2米.
∴AC=
| 102-62 |
∵梯子的顶端下滑1m,
∴AD=1m,

∴CD=8-1=7(m),
∴CE=
| DE2-CD2 |
| 102-72 |
| 51 |
∴BE=CE-BC=(
| 51 |
答:梯子的底端水平滑动(
| 51 |
(2)∵梯子的底端水平向外滑动1m,
∴CE=BC+BE=6+1=7,
∴CD=
| DE2+CE2 |
| 102+72 |
| 51 |
∴AD=AC-CD=(10-
| 51 |
答:梯子的顶端向下滑动(10-
| 51 |
(3)∵梯子顶端向下滑动的距离等于底端向外滑动的距离,
∴设AD=BE=x,则BC2+AC2=CD2+CE2,即62+82=(8-x)2+(6+x)2,解得x=2(m).
答:滑动的距离是2米.
点评:本题考查的是勾股定理的应用,熟知直角三角形的性质是解答此题的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
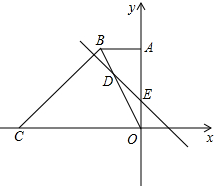 如图,在平面直角坐标系中,直角梯形OABC的边OC、OA分别与x轴、y轴重合,AB∥OC,∠AOC=90°,∠BCO=45°,BC=6,点C的坐标为(-9,0).
如图,在平面直角坐标系中,直角梯形OABC的边OC、OA分别与x轴、y轴重合,AB∥OC,∠AOC=90°,∠BCO=45°,BC=6,点C的坐标为(-9,0).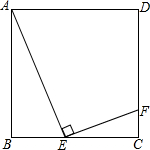 如图,已知边长为1的正方形ABCD,在BC边上有一动点E,连接AE,作EF⊥AE,交CD边于点F.
如图,已知边长为1的正方形ABCD,在BC边上有一动点E,连接AE,作EF⊥AE,交CD边于点F.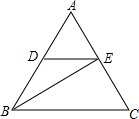 如图,在△ABC中,D是AB上一点,AB=3AD,DE∥BC,交AC于点E,若△ABC的面积为6,求△BED的面积.
如图,在△ABC中,D是AB上一点,AB=3AD,DE∥BC,交AC于点E,若△ABC的面积为6,求△BED的面积.