题目内容
6.在等边△ABC中,点E是AB上的动点,点E与点A、B不重合,点D在CB的延长线上,且EC=ED.(1)如图1,若点E是AB的中点,求证:BD=AE;
(2)如图2,若点E不是AB的中点时,(1)中的结论“BD=AE”能否成立?若不成立,请直接写出BD与AE数理关系,若成立,请给予证明.

分析 (1)由等边三角形的性质得出AE=BE,∠BCE=30°,再根据ED=EC,得出∠D=∠BCE=30°,再证出∠D=∠DEB,得出DB=BE,从而证出AE=DB;
(2)作辅助线得出等边三角形AEF,得出AE=EF,再证明三角形全等,得出DB=EF,证出AE=DB.
解答 (1)证明:∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,
∵点E是AB的中点,
∴CE平分∠ACB,AE=BE,
∴∠BCE=30°,
∵ED=EC,
∴∠D=∠BCE=30°.
∵∠ABC=∠D+∠BED,
∴∠BED=30°,
∴∠D=∠BED,
∴BD=BE.
∴AE=DB.
(2)解:AE=DB;
理由:过点E作EF∥BC交AC于点F.如图2所示:
∴∠AEF=∠ABC,∠AFE=∠ACB.
∵△ABC是等边三角形,
∴∠ABC=∠ACB=∠A=60°,AB=AC=BC,
∴∠AEF=∠ABC=60°,∠AFE=∠ACB=60°,
即∠AEF=∠AFE=∠A=60°,
∴△AEF是等边三角形.
∴∠DBE=∠EFC=120°,∠D+∠BED=∠FCE+∠ECD=60°,
∵DE=EC,
∴∠D=∠ECD,
∴∠BED=∠ECF.
在△DEB和△ECF中,
$\left\{\begin{array}{l}{∠DEB=∠ECF}\\{∠DBE=∠EFC}\\{DE=EC}\end{array}\right.$,
∴△DEB≌△ECF(AAS),
∴DB=EF,
∴AE=BD.
点评 本题考查了等边三角形的性质与判定、三角形的外角以及全等三角形的判定与性质;证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
17.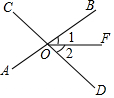 如图,直线AB、CD相交于点O,∠AOC=80°,∠2=45°,则∠1的度数为( )
如图,直线AB、CD相交于点O,∠AOC=80°,∠2=45°,则∠1的度数为( )
 如图,直线AB、CD相交于点O,∠AOC=80°,∠2=45°,则∠1的度数为( )
如图,直线AB、CD相交于点O,∠AOC=80°,∠2=45°,则∠1的度数为( )| A. | 70° | B. | 45° | C. | 35° | D. | 30° |
14.下列算式中,运算结果为负数的是( )
| A. | -(-1) | B. | |-1| | C. | (-1)2 | D. | (-1)3 |
11.下列四个图案中,是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
8.某校初一数学兴趣小组利用同一块木板,测量小车从不同高度沿斜放的木板从顶部滑到底部所用的时间,支撑物的高度h(cm)与小车下滑时间t(s)之间的关系如表所示:
根据表格提供的信息,下列说法错误的是( )
| 支撑物高度h/cm | 10 | 20 | 30 | 40 | 50 | 60 | 70 |
| 小车下滑时间t/s | 4.23 | 3.00 | 2.45 | 2.13 | 1.89 | 1.71 | 1.59 |
| A. | 支撑物的高度为40cm,小车下滑时间为2.13s | |
| B. | 支撑物高度h越大,小车下滑时间t越小 | |
| C. | 若小车下滑时间为2s,则支撑物高度在40cm至50cm之间 | |
| D. | 若支撑物的高度为80cm,则小车下滑时间可以使小于1.59s的任意值 |
 如图,△ABC是等边三角形,中线BD,CE相交于点O,则∠BOC=120°.
如图,△ABC是等边三角形,中线BD,CE相交于点O,则∠BOC=120°.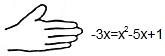 老师在黑板上写了一个正确的计算过程,随后用手捂住了一个二次三项式,形式如下:
老师在黑板上写了一个正确的计算过程,随后用手捂住了一个二次三项式,形式如下: