Question

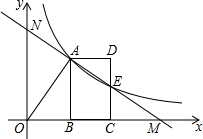如图，反比例函y=

k

x

（x＞0）的图象经过线段OA的端点A，O为原点，作AB⊥x轴于点B．
（1）若点B的坐标为（2，0），AB=3，则k得值为

 

．
（2）在1的条件下，将线段AB沿x轴正方向平移到线段DC的位置，反比例函y=

k

x

（x＞0）的图象恰好经过DC的中点E，直线AE与x轴交于M点，与y轴交于点N．
①求直线AE的函数表达式；
②探索线段AN与线段ME的大小关系，写出你的结论并说明理由．

Answer 1

考点：反比例函数综合题

专题：

分析：（1）由点B的坐标为（2，0），AB=3，AB⊥x轴，可得点A（2，3），然后利用待定系数法求得k的值；
（2）①由平移的性质，可求得CD的长，又由E是DC的中点，可求得点E的坐标，然后设AE的解析式为：y=kx+b，利用待定系数法即可求得直线AE的函数表达式；
②由①可求得点M，N的坐标，继而求得线段AN与线段ME的长，即可得AN=ME．

解答：解：（1）点B的坐标为（2，0），AB=3，AB⊥x轴，
∴点A（2，3），
∵反比例函y=

k

x

（x＞0）的图象经过线段OA的端点A，
∴3=

k

2

，
解得：k=6，
故答案为：6；

（2）①∵在（1）的条件下，将线段AB沿x轴正方向平移到线段DC的位置，
∴CD=AB=3，
∵E是DC的中点，
∴CE=

3

2

，
∵点C在反比例函数y=

6

x

上，
∴

3

2

=

6

x

，
解得：x=4，
∴点E（4，

3

2

），
设直线AE的解析式为：y=kx+b，

2k+b=3 4k+b= 3 2

，
解得：

k=- 3 4 b= 9 2

，
∴直线AE的解析式为：y=-

3

4

x+

9

2

；

②AN=ME．
理由：∵直线AE与x轴交于M点，与y轴交于点N，
∴当x=0时，y=

9

2

，
∴N（0，

9

2

），
当y=0时，0=-

3

4

x+

9

2

，
解得：x=6，
∴M（6，0），
∴AN=

( 9 2 -3)2+(0-2)2

=

5

2

，ME=

(6-4)2+(0- 3 2 )2

=

5

2

，
∴AN=ME．

点评：此题属于反比例函数综合题，考查了待定系数求函数解析式、平移的性质以及两点间的距离．此题综合性较强，难度较大，注意掌握数形结合思想与方程思想的应用．