题目内容
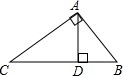 如图所示,△ABC中,∠BAC=90°,AD⊥BC于D.若AB=3,BC=5,则DC的长度是
如图所示,△ABC中,∠BAC=90°,AD⊥BC于D.若AB=3,BC=5,则DC的长度是考点:勾股定理
专题:
分析:在Rt△ABC中,根据勾股定理计算AC,易证得Rt△CAD∽Rt△CBA,根据相似三角形的性质得到CD:AC=AC:BC,即CD:4=4:5,即可求出CD.
解答:解:∵△ABC中,∠BAC=90°,AB=3,BC=5,
∴由勾股定理得:AC=4,
∵AD⊥BC,
∴∠ADC=90°,
而∠C公共,
∴Rt△CAD∽Rt△CBA,
∴CD:AC=AC:BC,即CD:4=4:5,
∴CD=
.
故答案为:
.
∴由勾股定理得:AC=4,
∵AD⊥BC,
∴∠ADC=90°,
而∠C公共,
∴Rt△CAD∽Rt△CBA,
∴CD:AC=AC:BC,即CD:4=4:5,
∴CD=
| 16 |
| 5 |
故答案为:
| 16 |
| 5 |
点评:本题考查了相似三角形的判定与性质:有两组角对应相等的两个三角形相似;相似三角形对应边的比相等.也考查了勾股定理.

练习册系列答案
相关题目
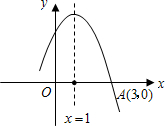 如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(3,0),且对称轴为x=1,给出下列四个结论:①b2-4ac>0;②bc<0;③2a+b=0;④a+b+c=0,其中正确结论的序号是
如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(3,0),且对称轴为x=1,给出下列四个结论:①b2-4ac>0;②bc<0;③2a+b=0;④a+b+c=0,其中正确结论的序号是
 如图,在四边形BCDE中,∠C=∠BED=90°,∠B=60°,延长CD、BE,得到Rt△ABC,已知CD=2,DE=1,则S△ABC=
如图,在四边形BCDE中,∠C=∠BED=90°,∠B=60°,延长CD、BE,得到Rt△ABC,已知CD=2,DE=1,则S△ABC=