题目内容
 如图,在四边形BCDE中,∠C=∠BED=90°,∠B=60°,延长CD、BE,得到Rt△ABC,已知CD=2,DE=1,则S△ABC=
如图,在四边形BCDE中,∠C=∠BED=90°,∠B=60°,延长CD、BE,得到Rt△ABC,已知CD=2,DE=1,则S△ABC=考点:解直角三角形
专题:
分析:求出∠A的度数,根据含30度角的直角三角形性质求出AD,求出AC,解直角三角形求出BC,即可求出答案.
解答:解:∵∠C=90°,∠B=60°,
∴∠A=30°,
∵∠AED=90°,DE=1,
∴AD=2DE=2,
∵CD=2,
∴AC=2+2=4,
∴tab60°=
,
∴BC=
=
,
∴S△ABC=
×AC×BC=
×4×
=
,
故答案为:
.
∴∠A=30°,
∵∠AED=90°,DE=1,
∴AD=2DE=2,
∵CD=2,
∴AC=2+2=4,
∴tab60°=
| 4 |
| BC |
∴BC=
| 4 |
| tan60° |
4
| ||
| 3 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
4
| ||
| 3 |
8
| ||
| 3 |
故答案为:
8
| ||
| 3 |
点评:本题考查了解直角三角形,含30度角的直角三角形性质,三角形面积的应用,解此题的关键是求出BC的长.

练习册系列答案
相关题目
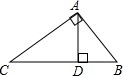 如图所示,△ABC中,∠BAC=90°,AD⊥BC于D.若AB=3,BC=5,则DC的长度是
如图所示,△ABC中,∠BAC=90°,AD⊥BC于D.若AB=3,BC=5,则DC的长度是 如图,在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C.请完成下列填空:
如图,在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C.请完成下列填空: 蓄水池中装有一个进水管和一个出水管,单位时间内进、出水量都一定,先打开进水管10分钟后再两管同时开放12分钟,然后关闭进水管,直至把池中的水放完.池中的蓄水量y(升)随时间x(分)变化的图象如图所示,则池中的水放完的时间是( )
蓄水池中装有一个进水管和一个出水管,单位时间内进、出水量都一定,先打开进水管10分钟后再两管同时开放12分钟,然后关闭进水管,直至把池中的水放完.池中的蓄水量y(升)随时间x(分)变化的图象如图所示,则池中的水放完的时间是( )