题目内容
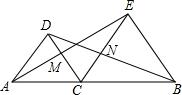 如图,△DAC和△EBC均是等边三角形,AE、BD分别与CD、CE交于点M、N,有如下结论:①△ACE≌△DCB;②△ACM≌△DCN;③CM=CN.其中,正确的是
如图,△DAC和△EBC均是等边三角形,AE、BD分别与CD、CE交于点M、N,有如下结论:①△ACE≌△DCB;②△ACM≌△DCN;③CM=CN.其中,正确的是考点:全等三角形的判定与性质,等边三角形的判定与性质
专题:
分析:根据等边三角形的性质可得AC=CD,BC=CE,∠ACD=∠BCE=60°,然后求出∠ACE=∠DCB=120°,再利用“边角边”证明△ACE和△DCB全等,从而判断出①正确;根据全等三角形对应角相等可得∠CAE=∠CDB,再求出∠DCN=∠ACM=60°,利用“角边角”证明△ACM和△DCN全等,判断出②正确;根据全等三角形对应边相等可得CM=CN,判断出③正确.
解答:解:∵△DAC和△EBC均是等边三角形,
∴AC=CD,BC=CE,∠ACD=∠BCE=60°,
∴∠ACE=∠DCB=120°,
在△ACE和△DCB中,
,
∴△ACE≌△DCB(SAS),故①正确;
∴∠CAE=∠CDB,
∵∠DCN=180°-60°×2=60°,
∴∠DCN=∠ACM=60°,
在△ACM和△DCN中,
,
∴△ACM≌△DCN(ASA),故②正确,
∴CM=CN,故③正确;
综上所述,正确的是①②③.
故答案为:①②③.
∴AC=CD,BC=CE,∠ACD=∠BCE=60°,
∴∠ACE=∠DCB=120°,
在△ACE和△DCB中,
|
∴△ACE≌△DCB(SAS),故①正确;
∴∠CAE=∠CDB,
∵∠DCN=180°-60°×2=60°,
∴∠DCN=∠ACM=60°,
在△ACM和△DCN中,
|
∴△ACM≌△DCN(ASA),故②正确,
∴CM=CN,故③正确;
综上所述,正确的是①②③.
故答案为:①②③.
点评:本题考查了全等三角形的判定与性质,等边三角形的性质,熟练掌握三角形全等的判断方法并根据度数相等得到相等的角是解题的关键.

练习册系列答案
相关题目
 将一张矩形纸对折再对折,然后沿着如图中的虚线剪下,打开,这个图形一定是一个(
将一张矩形纸对折再对折,然后沿着如图中的虚线剪下,打开,这个图形一定是一个(| A、三角形 | B、矩形 |
| C、菱形 | D、正方形 |
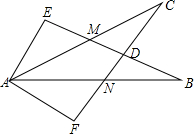 如图,已知∠E=∠F=90°,∠EAM=∠FAN,AE=AF,求证:CM=BN.
如图,已知∠E=∠F=90°,∠EAM=∠FAN,AE=AF,求证:CM=BN.