题目内容
7.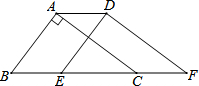 如图,在△ABC中,∠BAC=90°,AB=3,AC=4,BC=5,将△ABC沿直线BC向右平移2个单位得到△DEF,连接AD,则下列结论:
如图,在△ABC中,∠BAC=90°,AB=3,AC=4,BC=5,将△ABC沿直线BC向右平移2个单位得到△DEF,连接AD,则下列结论:①AC∥DF,AC=DF
②ED⊥DF
③四边形ABFD的周长是16
④点B到线段DF的距离是4.2
其中结论正确的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 直接根据平移的性质可对①进行判断;根据平移的性质得∠EDF=∠BAC=90°,则可对②进行判断;根据平移的性质得AD=BE=2,EF=BC=5,则可计算出四边形ABFD的周长.从而对③进行判断;延长BA交FD的延长线于H,如图,根据平移的性质证明BH⊥CH,再证明△HAD∽△HBF,利用相似比计算出AH,然后计算出BH即可对④进行判断.
解答 解:∵△ABC沿直线BC向右平移2个单位得到△DEF,
∴AC∥DF,AC=DF=4,所以①正确;
∠EDF=∠BAC=90°,
∴DE⊥DF,所以②正确;
∵△ABC沿直线BC向右平移2个单位得到△DEF,
∴AD=BE=2,EF=BC=5,
∴四边形ABFD的周长=AB+BE+EF+DF+AD=3+2+5+4+2=16,所以③正确,
延长BA交FD的延长线于H,如图,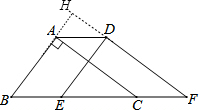
∵AC∥DF,AB⊥AC,
∴BH⊥CH,
∵AD∥BF,
∴△HAD∽△HBF,
∴$\frac{AH}{BH}$=$\frac{AD}{BF}$,即$\frac{AH}{AH+3}$=$\frac{2}{2+5}$,解得AH=1.2,
∴BH=BA+AH=3+1.2=4.2,
即点B到线段DF的距离是4.2,所以④正确.
故选D.
点评 本题考查了平移的性质:把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同;新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行且相等.也考查了相似三角形的判定与性质.

练习册系列答案
相关题目
2.如图是用火柴棍摆成的边长分别是1,2,3根火柴棍时的正方形,当边长为10根火柴棍时,摆出的正方形所用的火柴棍的根数为( )
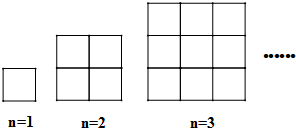

| A. | 220 | B. | 200 | C. | 120 | D. | 100 |
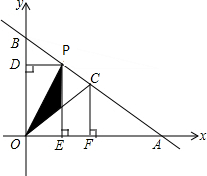 如图,点A,B坐标分别为(8,0)、(0,6),点C是线段AB的中点,点P是射线BA上一动点,过P作PD⊥y轴于D,PE⊥x轴于E,设OE=t,矩形OEPD与△POC重合部分的面积为S.
如图,点A,B坐标分别为(8,0)、(0,6),点C是线段AB的中点,点P是射线BA上一动点,过P作PD⊥y轴于D,PE⊥x轴于E,设OE=t,矩形OEPD与△POC重合部分的面积为S. 设函数y1=(x-k)2+k和y2=(x+k)2-k的图象相交于点A,函数y1,y2的图象的顶点分别为B和C.
设函数y1=(x-k)2+k和y2=(x+k)2-k的图象相交于点A,函数y1,y2的图象的顶点分别为B和C.