题目内容
16.若方程组$\left\{\begin{array}{l}{2x+3y=7}\\{5x-y=9}\end{array}\right.$的解是方程3x+my=-1的一个解,则m=-7.分析 求出方程组的解得到x与y的值,代入方程计算即可求出m的值.
解答 解:$\left\{\begin{array}{l}{2x+3y=7①}\\{5x-y=9②}\end{array}\right.$,
①+②×3得:17x=34,即x=2,
把x=2代入①得:y=1,
把x=2,y=1代入方程得:6+m=-1,
解得:m=-7,
故答案为:-7
点评 此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程都成立的未知数的值.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
6.抛物线y=-2x2-6x+1与x轴的交点个数是( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
7.用下列同一种多边形瓷砖铺设地平面,不能铺满地平面的是( )
| A. | 正三角形瓷砖 | B. | 长方形瓷砖 | C. | 正五边形瓷砖 | D. | 正六边形瓷砖 |
11.下列方程组中,是二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}{\frac{1}{x}+y=4}\\{x-y=1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{4x+3y=6}\\{2y+z=4}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=4}\\{x-y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=5}\\{{x}^{2}+{y}^{2}=13}\end{array}\right.$ |
8.下列四个等式从左至右的变形中,是因式分解的是( )
| A. | (a+1)(a-1)=a2-1 | B. | x2-2xy+y2-z2=(x-y)2-z2 | ||
| C. | ab-a-b+1=(a-1)(b-1) | D. | m2-2m-3=m(m-2-$\frac{3}{m}$) |
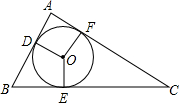 如图,⊙O是△ABC的内切圆,与AB,BC,CA分别切于点D,E,F,∠DOE=120°,∠EOF=150°,∠A=90°.
如图,⊙O是△ABC的内切圆,与AB,BC,CA分别切于点D,E,F,∠DOE=120°,∠EOF=150°,∠A=90°.