题目内容
15.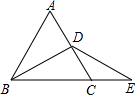 如图,在等边三角形ABC中,D是AC边上的中点,延长BC到点E,使CE=CD,则∠E的度数为( )
如图,在等边三角形ABC中,D是AC边上的中点,延长BC到点E,使CE=CD,则∠E的度数为( )| A. | 15° | B. | 20° | C. | 30° | D. | 40° |
分析 根据等边三角形的性质可得∠ACB=60°,∠CBD=30°,再根据等边对等角的性质求出∠E=∠CDE,然后根据三角形的一个外角等于与它不相邻的两个内角的和列式求解得到∠E的度数.
解答 解:∵△ABC是等边三角形,D是AC中点,
∴∠ACB=60°,∠CBD=30°,
∵CD=CE,
∴∠E=∠CDE,
∵∠BCD=∠E+∠CDE=2∠E=60°,
∴∠E=30°,
故选C.
点评 本题考查了等边三角形的性质,等腰三角形的判定,以及等边对等角,等角对等边的性质,利用外角的性质得到∠E的度数是解题的关键

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
14.平面直角坐标中,点M(0,-3)在( )
| A. | 第二象限 | B. | 第四象限 | C. | x轴上 | D. | y轴上 |
6.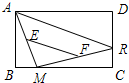 如图,矩形ABCD中,点R沿CD边从点C向点D运动,点M在BC边上运动,E、F分别是AM、MR的中点,则EF的长度随着点M、点R的运动( )
如图,矩形ABCD中,点R沿CD边从点C向点D运动,点M在BC边上运动,E、F分别是AM、MR的中点,则EF的长度随着点M、点R的运动( )
 如图,矩形ABCD中,点R沿CD边从点C向点D运动,点M在BC边上运动,E、F分别是AM、MR的中点,则EF的长度随着点M、点R的运动( )
如图,矩形ABCD中,点R沿CD边从点C向点D运动,点M在BC边上运动,E、F分别是AM、MR的中点,则EF的长度随着点M、点R的运动( )| A. | 变短 | B. | 变长 | C. | 不变 | D. | 无法确定 |
10.下列各式中去括号正确的是( )
| A. | a2-4(-a+1)=a2-4a-4 | B. | -(mn-1)+(m-n)=-mn-1+m-n | ||
| C. | 5x-(2x-1)-x2=5x-2x+1-x2 | D. | x2-2(2x-y+2)=x2-4x+y-2 |
20.下列各式中是二元一次方程的是( )
| A. | x+π=4 | B. | 2x-y | C. | 3x+y=0 | D. | 2x-5=y2 |
 如图,△ABC中,D、E分别是AB、AC边的中点,且DE=7cm,则BC=14 cm.
如图,△ABC中,D、E分别是AB、AC边的中点,且DE=7cm,则BC=14 cm. 如图,∠1、∠2、∠3、∠4、∠5.是五边形ABCDE的外角,则∠1+∠2+∠3+∠4+∠5=360°.
如图,∠1、∠2、∠3、∠4、∠5.是五边形ABCDE的外角,则∠1+∠2+∠3+∠4+∠5=360°.